题目内容
12.(1)计算:$\sqrt{4}+{(\frac{1}{2})^{-1}}$-2cos60°+(2-π)0(2)化简:$\frac{{{x^2}+{y^2}}}{x-y}-\frac{2xy}{x-y}$.
分析 (1)原式第一项利用算术平方根定义计算,第二项利用负整数指数幂法则计算,第三项利用特殊角的三角函数值计算,最后一项利用零指数幂法则计算即可得到结果;
(2)原式利用同分母分式的减法法则计算,约分即可得到结果.
解答 解:(1)原式=2+2-1+1=4;
(2)原式=$\frac{{x}^{2}+{y}^{2}-2xy}{x-y}$=$\frac{(x-y)^{2}}{x-y}$=x-y.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.下列根式中,属于最简二次根式的是( )
| A. | $\sqrt{0.5mn}$ | B. | $\sqrt{{a^2}+1}$ | C. | $\sqrt{27}$ | D. | $-\sqrt{125}$ |
20.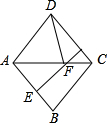 如图,在菱形ABCD中,∠BAD=100°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
如图,在菱形ABCD中,∠BAD=100°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
 如图,在菱形ABCD中,∠BAD=100°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
如图,在菱形ABCD中,∠BAD=100°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )| A. | 60° | B. | 50° | C. | 30° | D. | 20° |
17.若三角形两条边的长度分别是3cm和7cm,则第三条边的长度可能是( )
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 10cm |
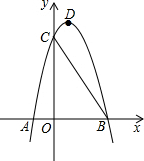 如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于点A(-2,0),B,与y轴交于点C,tan∠ABC=2.
如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于点A(-2,0),B,与y轴交于点C,tan∠ABC=2.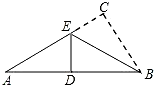 在Rt△ABC中,∠C=90°,当△ABC沿折痕BE翻折时,点C恰好落在AB的中点D上,若BE=4,则AC的长是( )
在Rt△ABC中,∠C=90°,当△ABC沿折痕BE翻折时,点C恰好落在AB的中点D上,若BE=4,则AC的长是( )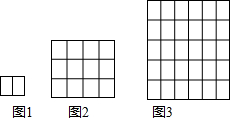 这样铺地板:第一块铺2块,如图1,第二次把第一次的完全围起来,如图2;第三次把第二次的完全围起来,如图3;…依次方法,铺第5次时需用34块木块才能把第四次所铺的完全围起来.
这样铺地板:第一块铺2块,如图1,第二次把第一次的完全围起来,如图2;第三次把第二次的完全围起来,如图3;…依次方法,铺第5次时需用34块木块才能把第四次所铺的完全围起来.