题目内容
18.观察方程①:x+$\frac{2}{x}$=3,方程②:x+$\frac{6}{x}$=5,方程③:x+$\frac{12}{x}$=7.写出第n个方程(系数用n表示):x+$\frac{n(n+1)}{x}$=2n+1;此方程解是:x=n或x=n+1.分析 观察已知方程,得出一般性规律,写出第n个方程,以及解即可.
解答 解:察方程①:x+$\frac{2}{x}$=3,方程②:x+$\frac{6}{x}$=5,方程③:x+$\frac{12}{x}$=7.写出第n个方程(系数用n表示):x+$\frac{n(n+1)}{x}$=2n+1;此方程解是:x=n或x=n+1,
故答案为:x+$\frac{n(n+1)}{x}$=2n+1;x=n或x=n+1
点评 此题考查了分式方程的解,弄清题中的规律是解本题的关键.

练习册系列答案
相关题目
13.若某三角形的三边分别是6cm、8cm、10cm,则分别连接三边中点所组成的三角形的周长是( )
| A. | 12cm | B. | 24cm | C. | 48cm | D. | 无法确定 |
 依语句画图并回答问题:已知:如图,△ABC.
依语句画图并回答问题:已知:如图,△ABC. 如图,三条直线两两相交于点O,∠AOE的对顶角是∠BOF,∠AOD的邻补角是∠AOC、∠DOB.
如图,三条直线两两相交于点O,∠AOE的对顶角是∠BOF,∠AOD的邻补角是∠AOC、∠DOB. 如图,AO⊥BO,直线CD经过点O,∠AOC=30°,求∠BOD的度数.
如图,AO⊥BO,直线CD经过点O,∠AOC=30°,求∠BOD的度数. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,若∠B=25°,则∠C的度数为40°.
如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,若∠B=25°,则∠C的度数为40°.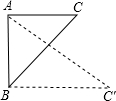 如图,等腰直角三角形ABC的直角边长为1.如果将斜边BC绕着点B顺时针旋转45°后得BC′,则tan∠BAC′=$\sqrt{2}$.
如图,等腰直角三角形ABC的直角边长为1.如果将斜边BC绕着点B顺时针旋转45°后得BC′,则tan∠BAC′=$\sqrt{2}$. 如图,在平行四边形EFGH中,它的周长为30,EF=6,则EH=9.
如图,在平行四边形EFGH中,它的周长为30,EF=6,则EH=9.