Question

7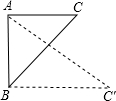．如图，等腰直角三角形ABC的直角边长为1．如果将斜边BC绕着点B顺时针旋转45°后得BC′，则tan∠BAC′=$\sqrt{2}$．

Answer 1

分析 首先利用勾股定理可求出BC的长，由旋转的性质可知：BC=BC'，∠CBC'=45°，结合等腰直角三角形的性质可推出∠ABC'=90°，进而可求出tan∠BAC′的值．

解答 解：
∵等腰直角三角形ABC的直角边长为1，
∴BC=$\sqrt{A{C}^{2}+A{B}^{2}}$=$\sqrt{2}$，∠ABC=45°
∵将斜边BC绕着点B顺时针旋转45°后得BC′，
∴BC=BC'=$\sqrt{2}$，∠CBC'=45°，
∴∠ABC′=45°+45°=90°，
∴tan∠BAC′=$\frac{BC′}{AB}=\frac{\sqrt{2}}{1}$=$\sqrt{2}$，
故答案为：$\sqrt{2}$．

点评 本题考查了旋转的性质、等腰直角三角形的性质以及勾股定理和锐角三角函数的运用，题目的综合性较强，是一道非常不错的中考题，熟记旋转的性质是解题的关键．