题目内容
求下列二次函数的对称轴和顶点坐标:y=2-2x2.
考点:二次函数的性质
专题:计算题
分析:先变形为顶点式y=-2x2+2,然后根据二次函数的性质求解.
解答:解:y=2-2x2
=-2x2+2,
所以抛物线的对称轴为y轴,顶点坐标为(0,2).
=-2x2+2,
所以抛物线的对称轴为y轴,顶点坐标为(0,2).
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.
当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
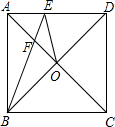 如图,正方形ABCD的边长为2,连接对角线AC、BD交于点O,∠ABD的角平分线交AC于点F,交AD于点E,连接OE,则△OEF的面积为( )
如图,正方形ABCD的边长为2,连接对角线AC、BD交于点O,∠ABD的角平分线交AC于点F,交AD于点E,连接OE,则△OEF的面积为( )A、
| ||||
B、
| ||||
C、3-2
| ||||
D、2
|
 已知:如图,正方形ABCD的边长我3,点E在BC上,CE=2BE,将正方形折叠,使点A与点E重合,折痕为MN,交AE于点G.求△ANE的面积.
已知:如图,正方形ABCD的边长我3,点E在BC上,CE=2BE,将正方形折叠,使点A与点E重合,折痕为MN,交AE于点G.求△ANE的面积. 如图,已知直线y=x+5与反比例函数y=
如图,已知直线y=x+5与反比例函数y=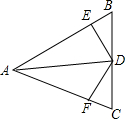 如图,AD平分线∠BAC,AE=AF,则下列说法:①△EAD≌△FAD;②∠AED=∠AFD;③BD=CD;④AD⊥BC.其中正确的有( )
如图,AD平分线∠BAC,AE=AF,则下列说法:①△EAD≌△FAD;②∠AED=∠AFD;③BD=CD;④AD⊥BC.其中正确的有( ) 如图,P、Q为反比例函数图象上的任意两点,过这两点分别向x轴、y轴作垂线,垂足分别为A、B,若S△AOP=2,则S△BOQ=
如图,P、Q为反比例函数图象上的任意两点,过这两点分别向x轴、y轴作垂线,垂足分别为A、B,若S△AOP=2,则S△BOQ=