题目内容
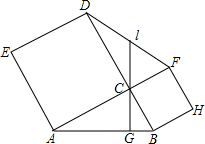 在△ABC中,∠ACB=90°,以AB、BC为边向△ABC外分别作正方形CBHF和正方形ACDE,连接DF,过点C作CG⊥AB,垂足为G,且CG的反向延长线与DF交于点I.
在△ABC中,∠ACB=90°,以AB、BC为边向△ABC外分别作正方形CBHF和正方形ACDE,连接DF,过点C作CG⊥AB,垂足为G,且CG的反向延长线与DF交于点I.(1)求证:CI=
| 1 |
| 2 |
| 1 |
| 2 |
(2)当∠ACB≠90°时,以上结论成立吗?若不成立,关系又怎样?
(3)若∠ACB是钝角,且分别向△ABC的形内作正方形ACDE及BCFH.问:此时线段CI与AB间的数量关系如何?
①CI是否平分DF?
②线段CI与
| 1 |
| 2 |
考点:全等三角形的判定与性质,平行四边形的判定与性质,矩形的判定与性质,正方形的性质
专题:
分析:(1)易证△DCF≌△ACB,可得∠CDF=∠CAB,∠CFD=∠CBA,DF=AB,即可证明∠ICD=∠IDC,可得CI=IF,即可解题;
(2)CI=
AB,CI≠
DF;理由:过D作DM∥CF交GC延长线于点M,易证∠CAG=∠DCM和∠MDC=∠ACB,即可证明△ACB≌△CDM,可得DM=BC,AB=CM,即可证明△DMI≌△FCI,可得CI=MI,即可解题;
(3)过F作MP∥CD,交AC于点M,交CI延长线于点P,易证∠CAB=∠CPF和∠ACB=∠PFC,即可证明△ACB≌△PFC,可得PF=AC,AB=PC,即可证明四边形CDPF为平行四边形,即可解题.
(2)CI=
| 1 |
| 2 |
| 1 |
| 2 |
(3)过F作MP∥CD,交AC于点M,交CI延长线于点P,易证∠CAB=∠CPF和∠ACB=∠PFC,即可证明△ACB≌△PFC,可得PF=AC,AB=PC,即可证明四边形CDPF为平行四边形,即可解题.
解答:证明:(1)∵△DCF和△ACB中,
,
∴△DCF≌△ACB,(SAS)
∴∠CDF=∠CAB,∠CFD=∠CBA,DF=AB,
∵CG⊥AB,
∴∠CAG+∠ACG=90°,
∵∠BCG+∠ACG=90°,
∴∠BCG=∠CAG,
∴∠ICD=∠IDC,
∴DI=CI,∠ICF=∠IFC,
∴CI=IF,
∴I是DF中点,
∴CI=
AB=
DF;
(2)CI=
AB,CI≠
DF;
理由:过D作DM∥CF交GC延长线于点M,如图1,
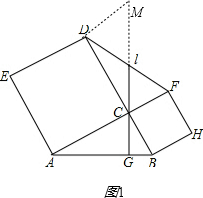
∵∠CAG+∠ACG=90°.∠ACG+∠DCM=90°,
∴∠CAG=∠DCM,
∵∠MDC+∠DCF=180°,∠ACB+∠DCF=180°,
∴∠MDC=∠ACB,
∵在△ACB和△CDM中,
,
∴△ACB≌△CDM,(ASA)
∴DM=BC,AB=CM,
∴DM=CF,
∵DM∥CF,
∴∠M=∠ICF,∠MDI=∠IFC,
∵在△DMI和△FCI中,
,
∴△DMI≌△FCI,(ASA)
∴CI=MI,
∴CI=
AB;
(3)过F作MP∥CD,交AC于点M,交CI延长线于点P,如图2,
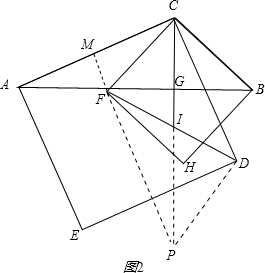
∵PM∥CD,CD⊥AC,
∴PM⊥AC,
∴∠CPF+∠PCA=90°,
∵∠CAB+∠ACP=90°,
∴∠CAB=∠CPF,
∵∠CFM+∠MCF=90°,∠CFM+∠PFH=90°,
∴∠PFH=∠MCF,
∵∠BCF=∠CFH=90°,
∴∠ACB=∠PFC,
∵在△ACB和△PFC中,
,
∴△ACB≌△PFC,(AAS)
∴PF=AC,AB=PC,
∵AC=CD,
∴PF=CD,
∴四边形CDPF为平行四边形,
∴CI平分DF,CI=
PC,
∴CI=
AB.
|
∴△DCF≌△ACB,(SAS)
∴∠CDF=∠CAB,∠CFD=∠CBA,DF=AB,
∵CG⊥AB,
∴∠CAG+∠ACG=90°,
∵∠BCG+∠ACG=90°,
∴∠BCG=∠CAG,
∴∠ICD=∠IDC,
∴DI=CI,∠ICF=∠IFC,
∴CI=IF,
∴I是DF中点,
∴CI=
| 1 |
| 2 |
| 1 |
| 2 |
(2)CI=
| 1 |
| 2 |
| 1 |
| 2 |
理由:过D作DM∥CF交GC延长线于点M,如图1,

∵∠CAG+∠ACG=90°.∠ACG+∠DCM=90°,
∴∠CAG=∠DCM,
∵∠MDC+∠DCF=180°,∠ACB+∠DCF=180°,
∴∠MDC=∠ACB,
∵在△ACB和△CDM中,
|
∴△ACB≌△CDM,(ASA)
∴DM=BC,AB=CM,
∴DM=CF,
∵DM∥CF,
∴∠M=∠ICF,∠MDI=∠IFC,
∵在△DMI和△FCI中,
|
∴△DMI≌△FCI,(ASA)
∴CI=MI,
∴CI=
| 1 |
| 2 |
(3)过F作MP∥CD,交AC于点M,交CI延长线于点P,如图2,

∵PM∥CD,CD⊥AC,
∴PM⊥AC,
∴∠CPF+∠PCA=90°,
∵∠CAB+∠ACP=90°,
∴∠CAB=∠CPF,
∵∠CFM+∠MCF=90°,∠CFM+∠PFH=90°,
∴∠PFH=∠MCF,
∵∠BCF=∠CFH=90°,
∴∠ACB=∠PFC,
∵在△ACB和△PFC中,
|
∴△ACB≌△PFC,(AAS)
∴PF=AC,AB=PC,
∵AC=CD,
∴PF=CD,
∴四边形CDPF为平行四边形,
∴CI平分DF,CI=
| 1 |
| 2 |
∴CI=
| 1 |
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中每一问构建全等三角形并求证是解题的关键.

练习册系列答案
相关题目
代数式-7,x,x2y,
,-5a2b3,
中,单项式有( )个.
| x+y |
| 2 |
| 1 |
| y |
| A、3 | B、4 | C、5 | D、6 |
 如图,∠B=∠E=90°,AB=CE,AC=CD,∠D=60°,CD=8cm.求:
如图,∠B=∠E=90°,AB=CE,AC=CD,∠D=60°,CD=8cm.求: