题目内容
15.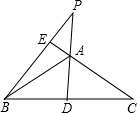 如图,在等腰三角形ABC中,AD、BE分别是底边BC和腰AC上的高线,DA、BE的延长线交于点P.若∠BAC=110°,求∠P的度数.
如图,在等腰三角形ABC中,AD、BE分别是底边BC和腰AC上的高线,DA、BE的延长线交于点P.若∠BAC=110°,求∠P的度数.
分析 根据等腰三角形的性质可得∠DAB=∠DAC=55°,根据对顶角相等可得∠EAP=55°,再根据高的定义和直角三角形的性质可求∠P的度数.
解答 解:∵△ABC是等腰三角形,AB=AC,AD⊥BC,∠BAC=110°,
∴∠DAB=∠DAC=55°,
∵∠DAC=∠EAP(对顶角相等),
∴∠EAP=∠DAC=55°,
又∵BE是腰AC上的高,
∴∠P=90°-∠EAP=90°-55°=35°.
故∠P的度数是35°.
点评 考查了等腰三角形的性质:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.

练习册系列答案
相关题目
6.在同一直角坐标系中,P、Q分别是y=-x+3与y=3x-5的图象上的点,且P、Q关于x轴对称,则点P的坐标是( )
| A. | (-$\frac{1}{2}$,$\frac{7}{2}$) | B. | (-2,5) | C. | (1,2) | D. | (-4,7) |
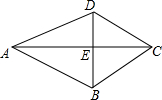 如图,△ADE≌△ABE,△DCE≌△BCE,求证:△ADC≌△ABC.
如图,△ADE≌△ABE,△DCE≌△BCE,求证:△ADC≌△ABC.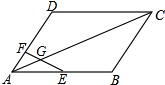 如图,在?ABCD中,E为AB的中点,点F在AD上,EF交AC于点G,AF=2,DF=4,AG=3,求AC的长.
如图,在?ABCD中,E为AB的中点,点F在AD上,EF交AC于点G,AF=2,DF=4,AG=3,求AC的长.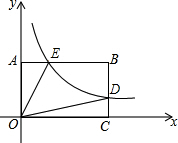 如图,反比例函数y=$\frac{k}{x}$(k>0)图象过矩形OABC边BC中点D交AB于点E,四边形ODBE的面积为2,则结论:①S△OAE=S△OCD;②E为AB中点;③k=2;④AO=AE,其中正确的序号为①②③.
如图,反比例函数y=$\frac{k}{x}$(k>0)图象过矩形OABC边BC中点D交AB于点E,四边形ODBE的面积为2,则结论:①S△OAE=S△OCD;②E为AB中点;③k=2;④AO=AE,其中正确的序号为①②③.