题目内容
14.若m<-2,则下列函数:①y=$\frac{m}{x}$(x>0);②y=-mx+1;③y=mx;④y=(m+1)x-1中y随x的增大而增大的函数是①②.(填序号)分析 ①由m<-2,利用反比例函数的性质可得出当x>0时,函数y=$\frac{m}{x}$中y随x的增大而增大;②由m<-2,利用一次函数的性质可得出函数y=-mx+1中y随x的增大而增大;③由m<-2,利用正比例函数的性质可得出函数y=mx中y随x的增大而减小;④由m<-2可得出m+1<-1,利用反比例函数的性质可得出函数y=(m+1)x-1在第二、四象限内y随x的增大而增大.综上即可得出结论.
解答 解:①∵m<-2,
∴当x>0时,函数y=$\frac{m}{x}$中y随x的增大而增大;
②∵m<-2,
∴-m>2,
∴函数y=-mx+1中y随x的增大而增大;
③∵m<-2,
∴函数y=mx中y随x的增大而减小;
④∵m<-2,
∴m+1<-1,
∴函数y=(m+1)x-1在第二、四象限内y随x的增大而增大.
综上所述:y随x的增大而增大的函数是①②.
故答案为:①②.
点评 本题考查了反比例函数的性质、一次函数的性质以及正比例函数的性质,根据反比例(正比例、一次)函数的性质逐一分析四个函数的增减性是解题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
15.若x-$\frac{1}{x}$=3,则$\frac{{x}^{2}}{{x}^{4}+1}$=( )
| A. | 11 | B. | 7 | C. | $\frac{1}{11}$ | D. | $\frac{1}{7}$ |
4.点P1(x1,y1)、P2(x2,y2)是一次函数y=5x+10的图象上两点,且x1<x2,则y1-y2( )
| A. | 大于0 | B. | 大于或等于0 | C. | 小于0 | D. | 小于或等于0 |
 如图,利用函数图象解方程组$\left\{\begin{array}{l}{x+2y=4}\\{2x-y=3}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
如图,利用函数图象解方程组$\left\{\begin{array}{l}{x+2y=4}\\{2x-y=3}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.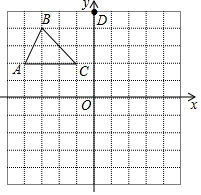 如图所示的网格中,每个小正方形的边长都是1,△ABC的三个顶点都在格点上,点A(-4,2),点D(0,5).
如图所示的网格中,每个小正方形的边长都是1,△ABC的三个顶点都在格点上,点A(-4,2),点D(0,5).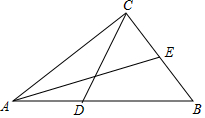 如图,在△ABC中,D为AB边上一动点,E为BC边上一点,∠BCD=∠BDC.
如图,在△ABC中,D为AB边上一动点,E为BC边上一点,∠BCD=∠BDC.