题目内容
9.已知二元一次方程组$\left\{\begin{array}{l}{x-y=-5}\\{x+2y=-2}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-4}\\{y=1}\end{array}\right.$,则在同一平面直角坐标系中,直线l1:y=x+5与+2y=-2直线l2:y=-$\frac{1}{2}$x-1的交点坐标为(-4,1).分析 二元一次方程可以化为一次函数,两个二元一次方程组的解就是两个函数的交点坐标.
解答 解:∵二元一次方程组$\left\{\begin{array}{l}{x-y=-5}\\{x+2y=-2}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-4}\\{y=1}\end{array}\right.$,
∴直线l1:y=x+5与直线l2:y=-$\frac{1}{2}$x-1的交点坐标为(-4,1).
故答案为(-4,1).
点评 本题主要考查了一次函数与二元一次方程组,函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
10.为了了解某校七年级期末考试数学科各分数段成绩分布情况,从参加考试的900名学生中抽取300名考生的期末数学成绩进行统计分析,在这个问题中,样本是( )
| A. | 300 | |
| B. | 被抽取的300名学生 | |
| C. | 被抽取的300名考生的期末数学成绩 | |
| D. | 某校七年级期末900名学生的数学成绩 |
11.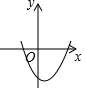 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a>0;②c>0;③b2-4ac>0;④-$\frac{b}{2a}$<0,正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a>0;②c>0;③b2-4ac>0;④-$\frac{b}{2a}$<0,正确的是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a>0;②c>0;③b2-4ac>0;④-$\frac{b}{2a}$<0,正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a>0;②c>0;③b2-4ac>0;④-$\frac{b}{2a}$<0,正确的是( )| A. | ①② | B. | ②④ | C. | ①③ | D. | ③④ |
4.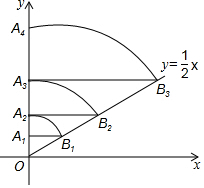 如图,直线l:y=$\frac{1}{2}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y 轴于点A3,…,按此做法进行下去,OA2017的长为( )
如图,直线l:y=$\frac{1}{2}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y 轴于点A3,…,按此做法进行下去,OA2017的长为( )
 如图,直线l:y=$\frac{1}{2}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y 轴于点A3,…,按此做法进行下去,OA2017的长为( )
如图,直线l:y=$\frac{1}{2}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y 轴于点A3,…,按此做法进行下去,OA2017的长为( )| A. | ($\sqrt{5}$)2016 | B. | ($\sqrt{5}$)2017 | C. | 22016 | D. | 22017 |



