题目内容
3.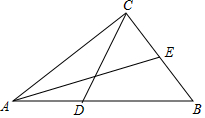 如图,在△ABC中,D为AB边上一动点,E为BC边上一点,∠BCD=∠BDC.
如图,在△ABC中,D为AB边上一动点,E为BC边上一点,∠BCD=∠BDC.(1)若∠BCD=70°,求∠ABC的度数;
(2)求证:∠EAB+∠AEB=2∠BDC.
分析 (1)由∠BCD=∠BDC=70°,利用三角形内角和定理即可求出∠ABC的度数;
(2)根据三角形内角和定理可得出∠EAB+∠AEB+∠ABE=180°、∠ABC+∠BCD+∠BDC=180°,进而可得出∠EAB+∠AEB=∠BCD+∠BDC,再根据∠BCD=∠BDC即可证出∠EAB+∠AEB=2∠BDC.
解答 解:(1)∵∠BCD=∠BDC=70°,
∴∠ABC=180°-∠BCD-∠BDC=40°.
(2)证明:∵∠EAB+∠AEB+∠ABE=180°,∠ABC+∠BCD+∠BDC=180°,
∴∠EAB+∠AEB=∠BCD+∠BDC.
又∵∠BCD=∠BDC,
∴∠EAB+∠AEB=2∠BDC.
点评 本题考查了三角形内角和定理,解题的关键是:(1)套用三角形内角和定理求出∠ABC的度数;(2)利用三角形内角和定理找出∠EAB+∠AEB=∠BCD+∠BDC.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
4. 一次函数y=(m-2)x+3的图象如图所示,则m的取值范围是( )
一次函数y=(m-2)x+3的图象如图所示,则m的取值范围是( )
 一次函数y=(m-2)x+3的图象如图所示,则m的取值范围是( )
一次函数y=(m-2)x+3的图象如图所示,则m的取值范围是( )| A. | m<2 | B. | 0<m<2 | C. | m<0 | D. | m>2 |
13.计算a2•a4的结果是( )
| A. | a6 | B. | 2a6 | C. | a8 | D. | 2a8 |
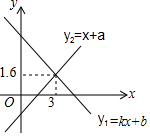 一次函数y1=kx+b与y2=x+a的图象如图所示,则关于x、y的方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=x+a}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=3}\\{y=1.6}\end{array}\right.$.
一次函数y1=kx+b与y2=x+a的图象如图所示,则关于x、y的方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=x+a}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=3}\\{y=1.6}\end{array}\right.$.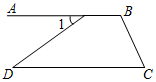 如图,若∠1=∠D=39°,∠C=51°,则∠B=129°.
如图,若∠1=∠D=39°,∠C=51°,则∠B=129°.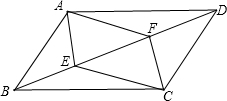 如图,在四边形ABCD中,AB∥CD,AD∥BC,现在请你添加一个适当的条件:BE=DF,使得四边形AECF为平行四边形(图中不再添加点和线).
如图,在四边形ABCD中,AB∥CD,AD∥BC,现在请你添加一个适当的条件:BE=DF,使得四边形AECF为平行四边形(图中不再添加点和线).