题目内容
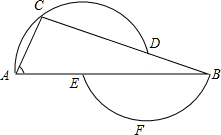 如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=66°,那么∠B=
如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=66°,那么∠B=考点:圆周角定理
专题:
分析:首先连接DE,由过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,根据圆内接四边形的性质可得:∠C+
∠AED=180°,继而可求得∠C=90°+
∠B,又由三角形内角和定理,即可求得答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答: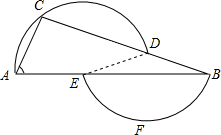 解:连接DE,
解:连接DE,
∵过D、A、C三点的圆的圆心为E,
∴∠C+
∠AED=180°,
∵过B、E、F三点的圆的圆心为D,
∴∠BED=∠B,
∴∠AED=180°-∠B,
∴∠C=90°+
∠B,
∵∠A+∠C+∠B=180°,
∴66°+90°+
∠B+∠B=180°,
解得:∠B=16°.
故答案为:16.
 解:连接DE,
解:连接DE,∵过D、A、C三点的圆的圆心为E,
∴∠C+
| 1 |
| 2 |
∵过B、E、F三点的圆的圆心为D,
∴∠BED=∠B,
∴∠AED=180°-∠B,
∴∠C=90°+
| 1 |
| 2 |
∵∠A+∠C+∠B=180°,
∴66°+90°+
| 1 |
| 2 |
解得:∠B=16°.
故答案为:16.
点评:此题考查了圆周角定理以及三角形内角和定理.此题难度适中,注意掌握辅助线的作法,注意数形结合与方程思想的应用.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
下列各式从左到右的变形中,属于因式分解的是( )
| A、(x-1)(x+1)=x2-1 |
| B、(a+b)2=a2+2ab+b2 |
| C、x2-x-2=(x+1)(x-2) |
| D、ax-ay-1=a(x-y)-1 |
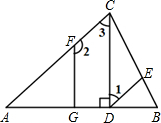 已知:在△ABC中,CD是AB边上的高,∠DEB=∠ACB,∠1+∠2=180°.试判断FG与AB的位置关系,并说明理由.请在下划线内补全解题过程或依据.
已知:在△ABC中,CD是AB边上的高,∠DEB=∠ACB,∠1+∠2=180°.试判断FG与AB的位置关系,并说明理由.请在下划线内补全解题过程或依据.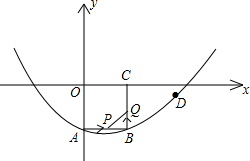 如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B和D(4,-
如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B和D(4,-