ΧβΡΩΡΎ»ί
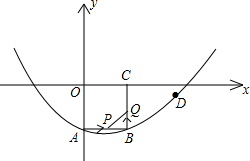 »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§’ΐΖΫ–ΈOABCΒΡ±Ώ≥ΛΈΣ2cmΘ§ΒψAΓΔCΖ÷±π‘Ύy÷αΒΡΗΚΑκ÷αΚΆx÷αΒΡ’ΐΑκ÷α…œΘ§≈ΉΈοœΏy=ax2+bx+cΨ≠ΙΐΒψAΓΔBΚΆDΘ®4Θ§-
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§’ΐΖΫ–ΈOABCΒΡ±Ώ≥ΛΈΣ2cmΘ§ΒψAΓΔCΖ÷±π‘Ύy÷αΒΡΗΚΑκ÷αΚΆx÷αΒΡ’ΐΑκ÷α…œΘ§≈ΉΈοœΏy=ax2+bx+cΨ≠ΙΐΒψAΓΔBΚΆDΘ®4Θ§-| 2 |
| 3 |
Θ®1Θ©«σ≈ΉΈοœΏΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©»γΙϊΒψP”…ΒψA≥ωΖΔ―ΊAB±Ώ“‘2cm/sΒΡΥΌΕ»œρΒψB‘ΥΕ·Θ§Ά§ ±ΒψQ”…ΒψB≥ωΖΔΘ§―ΊBC±Ώ“‘1cm/sΒΡΥΌΕ»œρΒψC‘ΥΕ·Θ§Β±Τδ÷–“ΜΒψΒΫ¥ο÷’Βψ ±Θ§Νμ“ΜΒψ“≤Υφ÷°ΆΘ÷Ι‘ΥΕ·Θ°…ηS=PQ2Θ®cm2Θ©Θ°
ΔΌ ‘«σ≥ωS”κ‘ΥΕ· ±Φδt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
ΔΎΒ±tΈΣΚΈ÷Β ±Θ§SΉν–ΓΘ§Ήν–Γ÷Β «Εύ…ΌΘΜ
Θ®3Θ©‘Ύ≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œ«σΒψMΘ§ ΙΒΟMΒΫDΓΔAΒΡΨύάκ÷°≤νΉν¥σΘ§«σ≥ωΒψMΒΡΉχ±ξΘ°
ΩΦΒψΘΚΕΰ¥ΈΚ· ΐΉέΚœΧβ
Ή®ΧβΘΚΉέΚœΧβ
Ζ÷ΈωΘΚΘ®1Θ©÷Μ–ηœ»«σ≥ωΒψAΓΔBΒΡΉχ±ξΘ§»ΜΚσ‘Ό‘Υ”Ο¥ΐΕ®œΒ ΐΖ®ΨΆΩ…ΫβΨωΈ ΧβΘΜ
Θ®2Θ©”…ΧβΩ…÷ΣΘΚAP=2tΘ§BQ=tΘ§PB=2-2tΘ§Θ®0ΓήtΓή1Θ©Θ°
ΔΌ‘ΎRtΓςPBQ÷–‘Υ”ΟΙ¥Ι…Ε®άμΦ¥Ω…ΒΟΒΫS”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
ΔΎ÷Μ–η‘Υ”Ο≈δΖΫΖ®ΨΆΩ…ΫβΨωΈ ΧβΘΜ
Θ®3Θ©ΗυΨί÷αΕ‘≥Τ–‘Ω…ΒΟMA=MBΘ§‘ρMD-MA=MD-MBΘ§»ΜΚσΗυΨίΝΫΒψ÷°ΦδœΏΕΈΉνΕΧΩ…ΒΟΘΚΒ±AΓΔDΓΔM»ΐΒψΙ≤œΏ ±Θ§MD-MBΘ®Φ¥MD-MAΘ©»ΓΒΫΉν¥σ÷ΒΘ§»ΜΚσ÷Μ–η«σ≥ω÷±œΏBDΒΡΫβΈω ΫΘ§ΨΆΩ…ΒΟΒΫ÷±œΏBD”κΕ‘≥Τ÷αx=1ΒΡΫΜΒψMΒΡΉχ±ξΘ°
Θ®2Θ©”…ΧβΩ…÷ΣΘΚAP=2tΘ§BQ=tΘ§PB=2-2tΘ§Θ®0ΓήtΓή1Θ©Θ°
ΔΌ‘ΎRtΓςPBQ÷–‘Υ”ΟΙ¥Ι…Ε®άμΦ¥Ω…ΒΟΒΫS”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
ΔΎ÷Μ–η‘Υ”Ο≈δΖΫΖ®ΨΆΩ…ΫβΨωΈ ΧβΘΜ
Θ®3Θ©ΗυΨί÷αΕ‘≥Τ–‘Ω…ΒΟMA=MBΘ§‘ρMD-MA=MD-MBΘ§»ΜΚσΗυΨίΝΫΒψ÷°ΦδœΏΕΈΉνΕΧΩ…ΒΟΘΚΒ±AΓΔDΓΔM»ΐΒψΙ≤œΏ ±Θ§MD-MBΘ®Φ¥MD-MAΘ©»ΓΒΫΉν¥σ÷ΒΘ§»ΜΚσ÷Μ–η«σ≥ω÷±œΏBDΒΡΫβΈω ΫΘ§ΨΆΩ…ΒΟΒΫ÷±œΏBD”κΕ‘≥Τ÷αx=1ΒΡΫΜΒψMΒΡΉχ±ξΘ°
Ϋβ¥πΘΚΫβΘΚΘ®1Θ©”…ΧβΩ…÷ΣΘΚΒψAΒΡΉχ±ξΈΣΘ®0Θ§-2Θ©Θ§ΒψBΒΡΉχ±ξΈΣΘ®2Θ§-2Θ©Θ§
ΓΏ≈ΉΈοœΏy=ax2+bx+cΨ≠ΙΐΒψAΘ®0Θ§-2Θ©ΓΔBΘ®2Θ§-2Θ©ΚΆDΘ®4Θ§-
Θ©Θ§
Γύ
Θ§
ΫβΒΟΘΚ
Θ°
Γύ≈ΉΈοœΏΒΡ±μ¥ο ΫΈΣy=
x2-
x-2Θ°
Θ®2Θ©”…ΧβΩ…÷ΣΘΚAP=2tΘ§BQ=tΘ§PB=2-2tΘ§Θ®0ΓήtΓή1Θ©Θ§
ΔΌ‘ΎRtΓςPBQ÷–Θ§
S=PQ2=PB2+BQ2=Θ®2-2tΘ©2+t2=5t2-8t+4Θ§
ΓύS”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΈΣS=5t2-8t+4Θ§Θ®0ΓήtΓή1Θ©ΘΜ
ΔΎS=5t2-8t+4=5Θ®t-
Θ©2+
Θ§
ΓΏ5ΘΨ0Θ§
ΓύΒ±t=
±Θ§S»ΓΉν–Γ÷ΒΈΣ
Θ°
Θ®3Θ©≈ΉΈοœΏy=
x2-
x-2ΒΡΕ‘≥Τ÷αΈΣx=-
=1Θ°
ΓΏAΘ®0Θ§-2Θ©Θ§BΘ®2Θ§-2Θ©Θ§
ΓύΒψAΓΔΒψBΙΊ”ΎΕ‘≥Τ÷αx=1Ε‘≥ΤΘ°
ΓΏΒψM‘ΎΕ‘≥Τ÷αx=1…œΘ§
ΓύMA=MBΘ§
ΓύMD-MA=MD-MBΘ°
ΗυΨίΝΫΒψ÷°ΦδœΏΕΈΉνΕΧΩ…ΒΟΘΚ
MDΓήMB+BDΘ§Φ¥MD-MBΓήBDΘ§
Β±AΓΔDΓΔM»ΐΒψΙ≤œΏ ±Θ§MD-MB»ΓΒΫΉν¥σ÷ΒΘ§Φ¥MD-MA»ΓΒΫΉν¥σ÷ΒΘ°
…η÷±œΏBDΒΡΫβΈω ΫΈΣy=mx+nΘ§
‘ρ
Θ§
ΫβΒΟΘΚ
Θ§
Γύ÷±œΏBDΒΡΫβΈω ΫΈΣy=
x-
Θ§
Β±x=1 ±Θ§y=
ΓΝ1-
=-
Θ§
ΓύΒψMΒΡΉχ±ξΈΣΘ®1Θ§-
Θ©Θ°
ΓΏ≈ΉΈοœΏy=ax2+bx+cΨ≠ΙΐΒψAΘ®0Θ§-2Θ©ΓΔBΘ®2Θ§-2Θ©ΚΆDΘ®4Θ§-
| 2 |
| 3 |
Γύ
|
ΫβΒΟΘΚ
|
Γύ≈ΉΈοœΏΒΡ±μ¥ο ΫΈΣy=
| 1 |
| 6 |
| 1 |
| 3 |
Θ®2Θ©”…ΧβΩ…÷ΣΘΚAP=2tΘ§BQ=tΘ§PB=2-2tΘ§Θ®0ΓήtΓή1Θ©Θ§
ΔΌ‘ΎRtΓςPBQ÷–Θ§
S=PQ2=PB2+BQ2=Θ®2-2tΘ©2+t2=5t2-8t+4Θ§
ΓύS”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΈΣS=5t2-8t+4Θ§Θ®0ΓήtΓή1Θ©ΘΜ
ΔΎS=5t2-8t+4=5Θ®t-
| 4 |
| 5 |
| 4 |
| 5 |
ΓΏ5ΘΨ0Θ§
ΓύΒ±t=
| 4 |
| 5 |
| 4 |
| 5 |
Θ®3Θ©≈ΉΈοœΏy=
| 1 |
| 6 |
| 1 |
| 3 |
-
| ||
2ΓΝ
|
ΓΏAΘ®0Θ§-2Θ©Θ§BΘ®2Θ§-2Θ©Θ§
ΓύΒψAΓΔΒψBΙΊ”ΎΕ‘≥Τ÷αx=1Ε‘≥ΤΘ°
ΓΏΒψM‘ΎΕ‘≥Τ÷αx=1…œΘ§
ΓύMA=MBΘ§
ΓύMD-MA=MD-MBΘ°
ΗυΨίΝΫΒψ÷°ΦδœΏΕΈΉνΕΧΩ…ΒΟΘΚ
MDΓήMB+BDΘ§Φ¥MD-MBΓήBDΘ§
Β±AΓΔDΓΔM»ΐΒψΙ≤œΏ ±Θ§MD-MB»ΓΒΫΉν¥σ÷ΒΘ§Φ¥MD-MA»ΓΒΫΉν¥σ÷ΒΘ°
…η÷±œΏBDΒΡΫβΈω ΫΈΣy=mx+nΘ§

‘ρ
|
ΫβΒΟΘΚ
|
Γύ÷±œΏBDΒΡΫβΈω ΫΈΣy=
| 2 |
| 3 |
| 10 |
| 3 |
Β±x=1 ±Θ§y=
| 2 |
| 3 |
| 10 |
| 3 |
| 8 |
| 3 |
ΓύΒψMΒΡΉχ±ξΈΣΘ®1Θ§-
| 8 |
| 3 |
ΒψΤάΘΚ±ΨΧβ÷ς“ΣΩΦ≤ιΝΥ”Ο¥ΐΕ®œΒ ΐΖ®«σ≈ΉΈοœΏΦΑ÷±œΏΒΡΫβΈω ΫΓΔ≈ΉΈοœΏΒΡ÷αΕ‘≥Τ–‘ΓΔΫβΖΫ≥ΧΉιΓΔΙ¥Ι…Ε®άμΓΔΝΫΒψ÷°ΦδœΏΕΈΉνΕΧΒ»÷Σ ΕΘ§‘Υ”Ο≈δΖΫΖ® «ΫβΨωΒΎΘ®2Θ©ΔΎ–ΓΧβΒΡΙΊΦϋΘ§‘Υ”Ο÷αΕ‘≥Τ–‘ΫΪMD-MAΉΣΜ·ΈΣMD-MB «ΫβΨωΒΎΘ®3Θ©–ΓΧβΒΡΙΊΦϋΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 Ά§≤ΫΝΖœΑ«ΩΜ·ΆΊ’ΙœΒΝ–¥πΑΗ
Ά§≤ΫΝΖœΑ«ΩΜ·ΆΊ’ΙœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
»γΙϊaΘΦbΘ§Ρ«Ο¥œ¬Ν–≤ΜΒ» Ϋ÷–ΨΏ”–Θ®ΓΓΓΓΘ©Ηω’ΐ»ΖΒΡΘ°
Θ®1Θ©a-3ΘΦb-3ΘΜΘ®2Θ©a-bΘΨb-bΘΜΘ®3Θ©a-aΘΦb-aΘΜΘ®4Θ©a+7ΘΨb-7Θ°
Θ®1Θ©a-3ΘΦb-3ΘΜΘ®2Θ©a-bΘΨb-bΘΜΘ®3Θ©a-aΘΦb-aΘΜΘ®4Θ©a+7ΘΨb-7Θ°
| AΓΔ1 | BΓΔ2 | CΓΔ3 | DΓΔ4 |
 ΝΫΩιΆξ»ΪœύΆ§ΒΡΒ»―ϋ»ΐΫ«–ΈΖ≈≥…»γΆΦ―υΉ”Θ§ΦΌ…ηΆΦ–Έ÷–ΒΡΥυ”–ΒψΓΔœΏΓΔΟφΕΦ‘ΎΆ§“ΜΤΫΟφΡΎΘ§÷Η≥ωΆΦ÷–œύΥΤ≤Μ’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©
ΝΫΩιΆξ»ΪœύΆ§ΒΡΒ»―ϋ»ΐΫ«–ΈΖ≈≥…»γΆΦ―υΉ”Θ§ΦΌ…ηΆΦ–Έ÷–ΒΡΥυ”–ΒψΓΔœΏΓΔΟφΕΦ‘ΎΆ§“ΜΤΫΟφΡΎΘ§÷Η≥ωΆΦ÷–œύΥΤ≤Μ’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©| AΓΔΓςDAEΓΉΓςDCA |
| BΓΔΓςEADΓΉΓςEBA |
| CΓΔΓςBADΓΉΓςCAE |
| DΓΔΓςBAEΓΉΓςCDA |
 »γΆΦΘΚ‘Ύ“ΜΧθ÷±œΏ…œΥ≥¥Έ»ΓAΓΔBΓΔC»ΐΒψΘ§“―÷ΣAB=5cmΘ§Βψ0 «œΏΕΈACΒΡ÷–ΒψΘ§«“OB=1.5cmΘ§‘ρBCΒΡ≥Λ «
»γΆΦΘΚ‘Ύ“ΜΧθ÷±œΏ…œΥ≥¥Έ»ΓAΓΔBΓΔC»ΐΒψΘ§“―÷ΣAB=5cmΘ§Βψ0 «œΏΕΈACΒΡ÷–ΒψΘ§«“OB=1.5cmΘ§‘ρBCΒΡ≥Λ «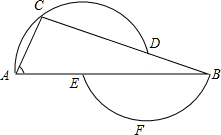 »γΆΦΘ§ΙΐDΓΔAΓΔC»ΐΒψΒΡ‘≤ΒΡ‘≤–ΡΈΣEΘ§ΙΐBΓΔEΓΔF»ΐΒψΒΡ‘≤ΒΡ‘≤–ΡΈΣDΘ§»γΙϊΓœA=66ΓψΘ§Ρ«Ο¥ΓœB=
»γΆΦΘ§ΙΐDΓΔAΓΔC»ΐΒψΒΡ‘≤ΒΡ‘≤–ΡΈΣEΘ§ΙΐBΓΔEΓΔF»ΐΒψΒΡ‘≤ΒΡ‘≤–ΡΈΣDΘ§»γΙϊΓœA=66ΓψΘ§Ρ«Ο¥ΓœB=