题目内容
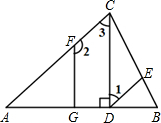 已知:在△ABC中,CD是AB边上的高,∠DEB=∠ACB,∠1+∠2=180°.试判断FG与AB的位置关系,并说明理由.请在下划线内补全解题过程或依据.
已知:在△ABC中,CD是AB边上的高,∠DEB=∠ACB,∠1+∠2=180°.试判断FG与AB的位置关系,并说明理由.请在下划线内补全解题过程或依据.解:FG⊥AB,理由如下:
∵∠DEB=∠ACB(
∴
∴∠1=∠3(
∵∠1+∠2=180°( 已知 )
∴∠3+∠2=180°(
∴
∵CD是AB边上的高(已知)
∴∠CDA=90°
∵FG∥CD
∴
∴FG⊥AB(
考点:平行线的判定与性质
专题:推理填空题
分析:先根据平行线的判定方法,由∠DEB=∠ACB得到AC∥DE,则根据平行线的性质得∠1=∠3,而∠1+∠2=180°,则∠3+∠2=180°,于是可判定FG∥CD,利用∠CDA=90°和平行线性质得∠FGA=∠CDA=90°,于是得到FG⊥AB.
解答:解:FG⊥AB,理由如下:
∵∠DEB=∠ACB,
∴AC∥DE,
∴∠1=∠3,
∵∠1+∠2=180°,
∴∠3+∠2=180°,
∴FG∥CD,
∵CD是AB边上的高,
∴∠CDA=90°,
∵FG∥CD,
∴∠FGA=∠CDA=90°,
∴FG⊥AB.
故答案为已知,AC∥DE,两直线平行,内错角相等,等量代换,FG∥CD,∠FGA=∠CDA,垂直的定义.
∵∠DEB=∠ACB,
∴AC∥DE,
∴∠1=∠3,
∵∠1+∠2=180°,
∴∠3+∠2=180°,
∴FG∥CD,
∵CD是AB边上的高,
∴∠CDA=90°,
∵FG∥CD,
∴∠FGA=∠CDA=90°,
∴FG⊥AB.
故答案为已知,AC∥DE,两直线平行,内错角相等,等量代换,FG∥CD,∠FGA=∠CDA,垂直的定义.
点评:本题考查了平行线的判定与性质:性质由形到数,用于推导角的关系并计算;判定由数到形,用于判定两直线平行.性质与判定的已知和结论正好相反,都是角的关系与平行线相关.

练习册系列答案
相关题目
根据等式的性质,下列变形正确的是( )
A、若x=y,则
| ||||
| B、若x=y,则x-2=2-y | ||||
| C、如果2x=y,那么-6x=-3y | ||||
D、如果
|
点P(3,m)到x轴的距离是4,则m的值为( )
| A、4 | B、±4 | C、-4 | D、无法确定 |
关于x的方程
+3=
有增根,则m的值为( )
| 7 |
| x-1 |
| m |
| x-1 |
| A、x=1 | B、x=-1 |
| C、x=7 | D、x=-7 |
如图所示的图案中不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
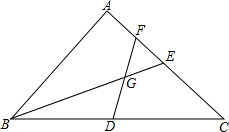 已知△ABC中,∠A=90°,AB=AC,D为BC中点,F,E为AC上两点,连接BE,DF交于△ABC内一点G,且∠EGF=45°.
已知△ABC中,∠A=90°,AB=AC,D为BC中点,F,E为AC上两点,连接BE,DF交于△ABC内一点G,且∠EGF=45°.
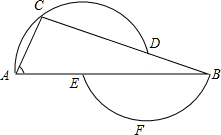 如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=66°,那么∠B=
如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=66°,那么∠B=