题目内容
若一个边长为a的正多边形的内角和等于720°,则这个正多边形的外接圆与内切圆的面积的比是 .
考点:正多边形和圆
专题:
分析:根据正多边形内角和公式可求得该多边形为正六边形,作出图形,可得△OAB是等边三角形,即可求得
的值,即可解题.
| OG |
| OA |
解答:解:∵正多边形内角和为180°(n-2),
∴180°(n-2)=720°,
解得:n=6,
∴各内角为
=120°,
作出图形,如下图,

则∠OAB=∠OBA=60°,
∴△OAB是等边三角形,
∴
=sin60°=
,
∴这个正多边形的外接圆与内切圆的面积的比=
=
,
答案为
.
∴180°(n-2)=720°,
解得:n=6,
∴各内角为
| 720° |
| 6 |
作出图形,如下图,

则∠OAB=∠OBA=60°,
∴△OAB是等边三角形,
∴
| OG |
| OA |
| ||
| 2 |
∴这个正多边形的外接圆与内切圆的面积的比=
| π•OA2 |
| π•OG2 |
| 4 |
| 3 |
答案为
| 4 |
| 3 |
点评:本题考查了正多边形内角和计算公式,考查了圆的面积的计算,本题中求得
的值是解题的关键.
| OG |
| OA |

练习册系列答案
相关题目

 如图:在一条直线上顺次取A、B、C三点,已知AB=5cm,点0是线段AC的中点,且OB=1.5cm,则BC的长是
如图:在一条直线上顺次取A、B、C三点,已知AB=5cm,点0是线段AC的中点,且OB=1.5cm,则BC的长是 如图,在△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,过点D作⊙O的切线FE交AC于点E.
如图,在△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,过点D作⊙O的切线FE交AC于点E.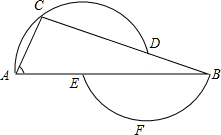 如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=66°,那么∠B=
如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=66°,那么∠B=