题目内容
12.在△ABC中,∠C=90°,BC=12cm,AB=20cm,求tanA和tanB的值.分析 首先根据勾股定理计算出AC的长,再根据正切定义可得答案.
解答  解:如图所示:
解:如图所示:
∵∠C=90°,BC=12cm,AB=20cm,
∴AC=$\sqrt{A{B}^{2}-C{B}^{2}}$=16cm,
∴tanA=$\frac{CB}{AC}$=$\frac{12}{16}$=$\frac{3}{4}$,
tanB=$\frac{AC}{BC}$=$\frac{16}{12}$=$\frac{4}{3}$.
点评 此题主要考查了锐角三角函数,关键是掌握正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.

练习册系列答案
相关题目
17.股民刘江上周五买进某公司股票1000股(周末开市),每股15.80元.下表是本周一至五每日该股票的涨跌情况(单位:元)(表中数据相对于前一天记录)
(1)周三的收盘价是多少?本周内最高价是每股多少元?
(2)已知刘江买进股票时付出成交额的0.15%的手续费好,卖出时付出了成交额的0.15%的手续费和成交额的0.1%的交易税,如果刘江在星期三刚好以收盘价将股票全部卖出,他的收益如何?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 涨跌 | +0.4 | +0.55 | -0.2 | +0.35 | -0.6 |
(2)已知刘江买进股票时付出成交额的0.15%的手续费好,卖出时付出了成交额的0.15%的手续费和成交额的0.1%的交易税,如果刘江在星期三刚好以收盘价将股票全部卖出,他的收益如何?
18. 如图,是一个正方体纸盒的展开图,若在其中三个正方形A、B、C中分别填入适当的数,使得它们折成正方体后相对的面上两个数互为相反数,则填入正方形A、B、C中的三个数依次是( )
如图,是一个正方体纸盒的展开图,若在其中三个正方形A、B、C中分别填入适当的数,使得它们折成正方体后相对的面上两个数互为相反数,则填入正方形A、B、C中的三个数依次是( )
 如图,是一个正方体纸盒的展开图,若在其中三个正方形A、B、C中分别填入适当的数,使得它们折成正方体后相对的面上两个数互为相反数,则填入正方形A、B、C中的三个数依次是( )
如图,是一个正方体纸盒的展开图,若在其中三个正方形A、B、C中分别填入适当的数,使得它们折成正方体后相对的面上两个数互为相反数,则填入正方形A、B、C中的三个数依次是( )| A. | -3、$-\frac{1}{2}$、1 | B. | $-\frac{1}{2}$、-3、1 | C. | 1、-3、$-\frac{1}{2}$ | D. | -3、1、$-\frac{1}{2}$ |
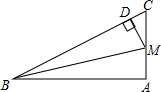 △ABC中,∠A=90°,M为AC的中点,MD⊥BC,D为垂足,说明:BD2-CD2=AB2.
△ABC中,∠A=90°,M为AC的中点,MD⊥BC,D为垂足,说明:BD2-CD2=AB2. 如图所示:AD平分∠BAC交BC于D,写出四条线段AB、BD、CD、AC之间的等量关系式$\frac{AB}{AC}=\frac{BD}{CD}$并证明你的结论.
如图所示:AD平分∠BAC交BC于D,写出四条线段AB、BD、CD、AC之间的等量关系式$\frac{AB}{AC}=\frac{BD}{CD}$并证明你的结论.