题目内容
2.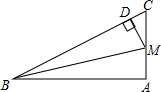 △ABC中,∠A=90°,M为AC的中点,MD⊥BC,D为垂足,说明:BD2-CD2=AB2.
△ABC中,∠A=90°,M为AC的中点,MD⊥BC,D为垂足,说明:BD2-CD2=AB2.
分析 先根据勾股定理得出BD2=BM2-MD2,MD2=MC2-CD2,BD2=AB2+AM2-MC2+CD2,再由M为AC的中点即可得出结论.
解答 证明:∵MD⊥BC,
∴BD2=BM2-MD2,MD2=MC2-CD2,
∴BD2=BM2-MC2+CD2.
∵∠A=90°,
∴BM2=AB2+AM2,
∴BD2=AB2+AM2-MC2+CD2,
∵M为AC的中点,
∴AM=MC,
∴AM2=MC2,
∴BD2=AB2+CD2,即BD2-CD2=AB2.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
11.下列说法正确的是( )
| A. | 在一个三角形中最多有两个锐角 | B. | 在一个三角形中最多有两个钝角 | ||
| C. | 在一个三角形中最多有两个直角 | D. | 在一个三角形中最少有两个锐角 |
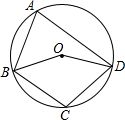 如图,A、B、C、D四点都在⊙O上,∠C=100°,则:
如图,A、B、C、D四点都在⊙O上,∠C=100°,则: 如图,在一块长和宽分别为a和b(a>b)的长方形黑板的四周,镶上宽度为x的木条.则这个新长方形的面积是ab+2ax+2bx+4x2.
如图,在一块长和宽分别为a和b(a>b)的长方形黑板的四周,镶上宽度为x的木条.则这个新长方形的面积是ab+2ax+2bx+4x2.