题目内容
16.先计算下列各式:$\sqrt{1}$=1,$\sqrt{1+3}$=2,$\sqrt{1+3+5}$=3,$\sqrt{1+3+5+7}$=4,$\sqrt{1+3+5+7+9}$=5.(1)通过观察并归纳,请写出:$\sqrt{1+3+5+…+(2n-1)}$=n.
(2)计算:$\sqrt{2+6+10+14+…+102}$=26$\sqrt{2}$.
分析 (1)先计算出各二次根式的值,根据计算结果找出其中的规律,然后用含n的式子表示;
(2)$\sqrt{2}$=$\sqrt{2}$,$\sqrt{2+6}$=$\sqrt{2+4×2-2}$=2$\sqrt{2}$,$\sqrt{2+6+10}$=$\sqrt{2+6+4×3-2}$=3$\sqrt{2}$,然后找出其中的规律进行计算即可.
解答 解:(1)$\sqrt{1}$=1;
$\sqrt{1+3}$=$\sqrt{1+(2×2-1)}$=2
$\sqrt{1+3+5}$=$\sqrt{1+3+(2×3-1)}$=3,
$\sqrt{1+3+5+7}$=$\sqrt{1+3+5+(2×4-1)}$=4,
$\sqrt{1+3+5+7+9}$=$\sqrt{1+3+5+7+(2×5-1)}$=5,
…
观察上述算式可知:$\sqrt{1+2+5+…+(2n-1)}$=n.
(2)$\sqrt{2}$=$\sqrt{2}$,
$\sqrt{2+6}$=$\sqrt{2+4×2-2}$=2$\sqrt{2}$,
$\sqrt{2+6+10}$=$\sqrt{2+6+4×3-2}$=3$\sqrt{2}$,
…
$\sqrt{2+6+10+14+…+102}$=$\sqrt{2+6+10+14+…+2×26-2}$=26$\sqrt{2}$.
故答案为:3;4;5;(1)n;(2)26$\sqrt{2}$.
点评 本题主要考查的是探索数字的变化规律,找出其中蕴含的规律是解题的关键.

练习册系列答案
相关题目
7.以下函数中,属于一次函数的是( )
| A. | $y=-\frac{x}{2}$ | B. | y=kx+b(k、b为常数) | C. | y=c(c为常数) | D. | $y=\frac{2}{x}$ |
4.下列各式中正确的是( )
| A. | ($\frac{1}{3}$)-2=-9 | B. | ($\frac{1}{3}$)-2=$\sqrt{3}$ | C. | ($\frac{1}{3}$)${\;}^{\frac{1}{2}}$=$\sqrt{3}$ | D. | 3${\;}^{-\frac{1}{2}}$=$\frac{\sqrt{3}}{3}$ |
1.-1100与(-1)100相比(n是自然数)( )
| A. | 前者大 | B. | 前者小 | C. | 两者相等 | D. | 大小取决于n |
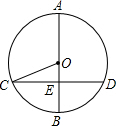 如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=26,CD=24,则$\frac{OE}{BE}$=$\frac{5}{8}$.
如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=26,CD=24,则$\frac{OE}{BE}$=$\frac{5}{8}$.