题目内容
6.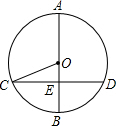 如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=26,CD=24,则$\frac{OE}{BE}$=$\frac{5}{8}$.
如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=26,CD=24,则$\frac{OE}{BE}$=$\frac{5}{8}$.
分析 根据垂径定理求出CE,求出OC、OB,根据勾股定理求出OE,求出BE,即可求出答案.
解答 解:如图:
∵AB是⊙O的直径,弦CD⊥AB,CD=24,
∴CE=$\frac{1}{2}$CD=12,∠OEC=90°,
∵AB=26,
∴OA=OB=OC=13,
由勾股定理得:OE=$\sqrt{O{C}^{2}-C{E}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
∴BE=13-5=8,
∴$\frac{OE}{BE}$=$\frac{5}{8}$,
故答案为:$\frac{5}{8}$.
点评 本题考查了垂径定理和勾股定理的应用,能根据垂径定理得出CE=$\frac{1}{2}$CD和OE的长是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.-$\root{3}{a}=\root{3}{{\frac{4}{5}}}$,则a的值为( )
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | $±\frac{4}{5}$ | D. | $-\frac{64}{125}$ |
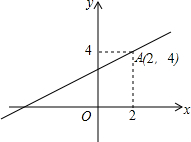 已知函数y=kx+3的图象经过点A(2,4).
已知函数y=kx+3的图象经过点A(2,4).