题目内容
 如图,△ABC中,AC=6cm,BC=8cm,AB=10cm,D、E、F分别是BC、AB、CA的中点,则△EDF的面积是
如图,△ABC中,AC=6cm,BC=8cm,AB=10cm,D、E、F分别是BC、AB、CA的中点,则△EDF的面积是考点:三角形中位线定理
专题:几何图形问题
分析:首先根据三角形的中位线定理求得EF、DE、DF的长,然后利用勾股定理的逆定理即可证明△DEF是直角三角形,从而求得面积.
解答:解:∵D、E分别是BC和AB的中点,
∴DE=
AC=3cm,
同理DF=5cm,EF=4cm,
∵32+42=52,
∴EF2+DE2=DF2,
∴△DEF是直角三角形,∠DEF=90°,
∴△EDF的面积是
DE•EF=
×3×4=6(cm2).
故答案是:6cm2.
∴DE=
| 1 |
| 2 |
同理DF=5cm,EF=4cm,
∵32+42=52,
∴EF2+DE2=DF2,
∴△DEF是直角三角形,∠DEF=90°,
∴△EDF的面积是
| 1 |
| 2 |
| 1 |
| 2 |
故答案是:6cm2.
点评:本题考查了三角形的中位线定理以及勾股定理的逆定理,正确证明△DEF是直角三角形是关键.

练习册系列答案
相关题目
下列统计中,能用“全面调查”的是( )
| A、某厂生产的电视机的使用寿命 |
| B、某校七年级学生的身高情况 |
| C、全国中学生的视力情况 |
| D、全国各地生产的矿泉水的合格率 |
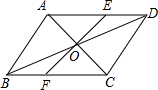 如图所示,过平行四边形ABCD对角线的交点0,分别交AD于点E,交BC于点F,若0E=5,四边形CDEF的周长为25,则平行四边形ABCD的周长为
如图所示,过平行四边形ABCD对角线的交点0,分别交AD于点E,交BC于点F,若0E=5,四边形CDEF的周长为25,则平行四边形ABCD的周长为 如图所示:
如图所示: 如图,
如图, 如图,在△ABC中,AB=AC=10cm,BC=12cm,AD为△ABC的中线,E,F为AD上的两点,则阴影部分的面积为
如图,在△ABC中,AB=AC=10cm,BC=12cm,AD为△ABC的中线,E,F为AD上的两点,则阴影部分的面积为