题目内容
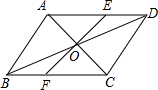 如图所示,过平行四边形ABCD对角线的交点0,分别交AD于点E,交BC于点F,若0E=5,四边形CDEF的周长为25,则平行四边形ABCD的周长为
如图所示,过平行四边形ABCD对角线的交点0,分别交AD于点E,交BC于点F,若0E=5,四边形CDEF的周长为25,则平行四边形ABCD的周长为考点:平行四边形的性质
专题:几何图形问题
分析:根据平行四边形的性质和中对称性,可知,?ABCD的周长为ED+CD+CF的2倍,只要求得ED+CD+CF,则?ABCD的周长即可求出.
解答:解:根据平行四边形的中心对称性得:OF=OE=5,
∵四边形CDEF的周长为25,
∴ED+CD+CF=25-10=15,
∴?ABCD的周长=15×2=30,
故答案为:30.
∵四边形CDEF的周长为25,
∴ED+CD+CF=25-10=15,
∴?ABCD的周长=15×2=30,
故答案为:30.
点评:此题主要考查了平行四边形的基本性质,并利用性质解题.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.平行四边形是中心对称图形.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 观察统计图,下列判断错误的是( )
观察统计图,下列判断错误的是( )| A、甲班男、女生人数相等 |
| B、乙班女生比男生人数多 |
| C、乙班女生比甲班女生人数多 |
| D、无法比较甲、乙两班女生人数谁多谁少 |
 如图,以点O为圆心,OB为半径画弧,交数轴于点A,若点A所表示的数为x,则x2-1的立方根为
如图,以点O为圆心,OB为半径画弧,交数轴于点A,若点A所表示的数为x,则x2-1的立方根为 某班有54人.其中参加读书活动的人数为18人,参加科技活动人数占全班人数的
某班有54人.其中参加读书活动的人数为18人,参加科技活动人数占全班人数的 如图,已知MN∥PQ,EF与MN,PQ分别交于A、C两点,过A、C两点作两组内错角的平分线,分别交于点B、D,则四边形ABCD是
如图,已知MN∥PQ,EF与MN,PQ分别交于A、C两点,过A、C两点作两组内错角的平分线,分别交于点B、D,则四边形ABCD是 如图,△ABC中,AC=6cm,BC=8cm,AB=10cm,D、E、F分别是BC、AB、CA的中点,则△EDF的面积是
如图,△ABC中,AC=6cm,BC=8cm,AB=10cm,D、E、F分别是BC、AB、CA的中点,则△EDF的面积是