Question

6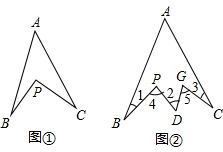．如图1，在∠A内部有一点P，连接BP，CP，请回答下列问题：
（1）求证：∠P=∠1+∠2+∠A；
（2）如图2，如果在BAC间有两个向上突起的角，请你根据前面的结论猜想∠1，∠2，∠3，∠4，∠5，∠A之间有什么等量关系？并说明理由．

Answer 1

分析 （1）作射线AP，如图①，根据三角形外角性质得∠3=∠1+∠BAP，∠4=∠CAP+∠2，然后把两式相加即可得到结论；
（2）作射线AP、AG，连结AD，如图②，利用（1）的结论得到，∠4=∠1+∠BAD+∠ADP，∠5=∠ADG+∠3+∠DAC，然后把两式相加可得∠4+∠5=∠1+∠2++∠3+∠A．

解答 （1）证明：作射线AP，如图①，
∵∠3=∠1+∠BAP，∠4=∠CAP+∠2，
∴∠3+∠4=∠1+∠BAP+∠CAP+∠2=∠1+∠2+∠A，
即∠P=∠1+∠2+∠A；
（2）解：∠4+∠5=∠1+∠2++∠3+∠A．理由如下：
作射线AP、AG，连结AD，如图②，
由（1）得∠4=∠1+∠BAD+∠ADP，∠5=∠ADG+∠3+∠DAC，
∴∠4+∠5=∠1+∠BAD+∠ADP+∠ADG+∠3+∠DAC=∠1+∠2+∠3+∠A．

点评 本题考查了三角形内角和定理：三角形内角和是180°．三角形内角和主要用在求三角形中角的度数．也考查了三角形外角性质．