题目内容
14.观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…(1)请根据你发现的规律填空:6×8+1=72;
(2)用含n的等式表示上面的规律:n(n+2)+1=(n+1)2;
(3)用找到的规律解决下面的问题:
计算:$(1+\frac{1}{1×3})(1+\frac{1}{2×4})(1+\frac{1}{3×5})…(1+\frac{1}{2013×2015})$.
分析 (1)(2)等式的左边是相差为2的两个数相乘,再加上1;右边是两个数的平均数的平方,由此规律得出答案即可;
(3)利用以上规律,计算交错约分得出答案即可.
解答 解:(1)∵1×3+1=4=22
2×4+1=9=32
3×5+1=16=42
4×6+1=25=52
…
∴6×8+1=72;
(2)由(1)可得出,第n个式子表达式为:n(n+2)+1=(n+1)2;
(3)原式=$\frac{1×3+1}{1×3}$×$\frac{2×4+1}{2×4}$×$\frac{3×5+1}{3×5}$×…×$\frac{2013×2015+1}{2013×2015}$
=$\frac{{2}^{2}}{1×3}$×$\frac{{3}^{2}}{2×4}$×$\frac{{4}^{2}}{3×5}$×…×$\frac{201{4}^{2}}{2013×2015}$
=$\frac{2×2014}{2015}$
=$\frac{4028}{2015}$.
点评 此题主要考查了数字变化规律,根据已知得出数字中的变与不变是解题关键.

练习册系列答案
相关题目
19.一元二次方程x2-x-1=0的两个实数根中较大的根是( )
| A. | 1+$\sqrt{5}$ | B. | $\frac{1+\sqrt{5}}{2}$ | C. | $\frac{1-\sqrt{5}}{2}$ | D. | $\frac{-1+\sqrt{5}}{2}$ |
3.下列图形不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
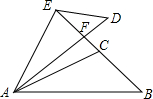 如图所示,△ABC≌△ADE,BC的延长线过点E,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,∠DEF的度数是35°.
如图所示,△ABC≌△ADE,BC的延长线过点E,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,∠DEF的度数是35°.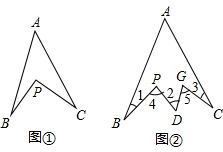 如图1,在∠A内部有一点P,连接BP,CP,请回答下列问题:
如图1,在∠A内部有一点P,连接BP,CP,请回答下列问题: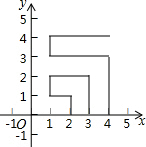 一个粒子从坐标系中的点(1,0)开始沿图方向跳动,第一次跳到(2,0)以后每次跳动一个单位长度,则第2014次跳动后所在位置的坐标为(45,10).
一个粒子从坐标系中的点(1,0)开始沿图方向跳动,第一次跳到(2,0)以后每次跳动一个单位长度,则第2014次跳动后所在位置的坐标为(45,10).