题目内容
1．已知抛物线y=x2-（k+2）x+9的顶点在坐标轴上，则k的值为4，-8，-2．分析 由于抛物线的顶点在坐标轴上，故应分在x轴上与y轴上两种情况进行讨论．
解答 解：当抛物线y=x2-（k+2）x+9的顶点在x轴上时，△=0，即△=（k+2）2-4×9=0，解得k=4或k=-8；
当抛物线y=x2-（k+2）x+9的顶点在y轴上时，x=-$\frac{b}{2a}$=$\frac{k+2}{2}$=0，解得k=-2．
故答案为：4，-8，-2．
点评 本题考查的是二次函数的性质，解答此题时要注意进行分类讨论，不要漏解．
练习册系列答案
相关题目
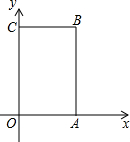如图，在矩形ABCD中，O为坐标原点，A，C两点坐标分别为（3，0）和（0，5）．
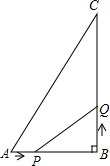如图，在△ABC中，AB=6cm，BC=12cm，∠B=90°．点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，如果P、Q分别从A、B同时出发，设移动时间为t（s）．
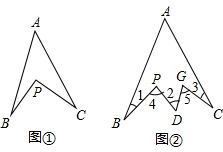如图1，在∠A内部有一点P，连接BP，CP，请回答下列问题：