题目内容
1.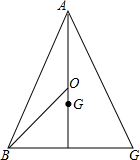 如图,已知△ABC,AB=AC=13厘米,BC=10厘米.O是△ABC的外心,G是△ABC的重心,求0G的长.
如图,已知△ABC,AB=AC=13厘米,BC=10厘米.O是△ABC的外心,G是△ABC的重心,求0G的长.
分析 由等腰三角形的性质得出AD⊥BC,BD=CD=$\frac{1}{2}$BC=5厘米,由勾股定理求出AD,由重心定理即可得出AG的长,设OA=OB=x厘米,则OD=(8-x)厘米,在Rt△OBD中,由勾股定理得出方程,解方程求出OA,即可得出0G的长.
解答 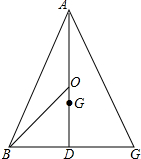 解:如图所示:
解:如图所示:
∵AB=AC,O是△ABC的外心,
∴AD⊥BC,BD=CD=$\frac{1}{2}$BC=5厘米,OA=OB,
由勾股定理得:AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12(厘米),
∵G是△ABC的重心,
由重心定理得:AG=$\frac{2}{3}$AD=$\frac{2}{3}$×12=8(厘米),
设OA=OB=x厘米,则OD=(8-x)厘米,
在Rt△OBD中,由勾股定理得:
52+(12-x)2=x2,
解得:x=$\frac{169}{24}$,
∴OA=$\frac{169}{24}$(厘米),
∴OG=AG-OA=8-$\frac{169}{24}$=$\frac{23}{24}$(厘米).
点评 本题考查了三角形的外心、等腰三角形的性质、勾股定理、重心定理;熟练掌握等腰三角形的性质,运用勾股定理和重心定理是解决问题的关键.

练习册系列答案
相关题目
11.若(x+2)2+|y-3|=0,则xy的值为( )
| A. | 6 | B. | -6 | C. | 8 | D. | -8 |
 如图所示,△ABC是等边三角形,AD=$\frac{1}{2}$AB,AD⊥CD,垂足为D,求证:AD∥BC.
如图所示,△ABC是等边三角形,AD=$\frac{1}{2}$AB,AD⊥CD,垂足为D,求证:AD∥BC.
 如图,A,B,C,D是⊙O上的点,且$\widehat{AC}=\widehat{BD}$.求证:AB∥CD.
如图,A,B,C,D是⊙O上的点,且$\widehat{AC}=\widehat{BD}$.求证:AB∥CD.