题目内容
9.已知(x2+y2+3)(x2+y2-2)-6=0,求x2+y2的值.分析 设t=x2+y2,则原方程转化为关于t的一元二次方程,通过解方程求得t即x2+y2的值.
解答 解:设t=x2+y2(t≥0),则由原方程得到:(t+3)(t-2)-6=0,
整理,得
(t+4)(t-3)=0,
解得t1=-4(舍去),t2=3,
所以x2+y2=3.
点评 本题考查了换元法解一元二次方程.即把某个式子看作一个整体,用一个字母去代替它,实行等量替换.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
20.x2-2ax+4a-3=0的两根均大于1,则实数a的取值范围是( )
| A. | a≥1 | B. | 0<a≤3 | C. | a≤3 | D. | a≥3 |
19.下列计算错误的是( )
| A. | (-2x)3=-2x3 | B. | -a2•a=-a3 | C. | (-x)9+(-x)9=-2x9 | D. | (-2a3)2=4a6 |
 一个工件的形状和部分尺寸如图所示,其体积为a(a+1)(5a+1)+(3a+2)(3a-2)-a+4,求工件的长x是多少(用含a的式子表示).
一个工件的形状和部分尺寸如图所示,其体积为a(a+1)(5a+1)+(3a+2)(3a-2)-a+4,求工件的长x是多少(用含a的式子表示).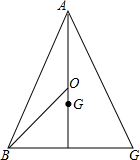 如图,已知△ABC,AB=AC=13厘米,BC=10厘米.O是△ABC的外心,G是△ABC的重心,求0G的长.
如图,已知△ABC,AB=AC=13厘米,BC=10厘米.O是△ABC的外心,G是△ABC的重心,求0G的长.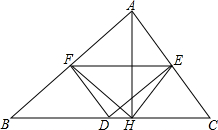 已知:如图,在△ABC中,AH⊥BC于点H,D,E,F分别是BC,AC,AB的中点.求证:△DEF≌△HFE.
已知:如图,在△ABC中,AH⊥BC于点H,D,E,F分别是BC,AC,AB的中点.求证:△DEF≌△HFE.