题目内容
 如图5×5的正方形网格图中,每小方格的边长都为1cm.在每个小格的顶点叫做格点,A,B为网格图中两个格点,分别按下列要求画出图形:
如图5×5的正方形网格图中,每小方格的边长都为1cm.在每个小格的顶点叫做格点,A,B为网格图中两个格点,分别按下列要求画出图形:(1)在如图网格图中,线段AB的长度为
(2)在如图网格图中,用直尺和圆规作一个以AB为底边的等腰直角三角形△ABC,使另一个顶点C也在格点上;此时△ABC的面积=
(3)在如图网格图中找到格点D使△ABD是等腰三角形,并标出点D的位置.这样的点D共有
考点:勾股定理,等腰三角形的判定,等腰直角三角形
专题:作图题
分析:(1)根据勾股定理计算即可求出AB的长;
(2)作AB的垂直平分线,利用三角形的面积公式计算即可;
(3)当AB、AD、BD分别为底时,求出符合题意的格点即可.
(2)作AB的垂直平分线,利用三角形的面积公式计算即可;
(3)当AB、AD、BD分别为底时,求出符合题意的格点即可.
解答: 解:(1)AB=
解:(1)AB=
=
cm,
(2)如图所示:S△ABC=2.5;
(3)如图所示:实心黑点为D的位置,共7个,
故答案为:
;2.5;7.
 解:(1)AB=
解:(1)AB=| 12+32 |
| 10 |
(2)如图所示:S△ABC=2.5;
(3)如图所示:实心黑点为D的位置,共7个,
故答案为:
| 10 |
点评:本题考查了勾股定理的运用,解题是需仔细分析题意,结合图形,利用勾股定理即可解决问题.

练习册系列答案
相关题目
 如图,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于点D,DE⊥AB于E.若△ADE的周长为8cm,则AB为( )
如图,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于点D,DE⊥AB于E.若△ADE的周长为8cm,则AB为( )| A、10cm | B、16cm |
| C、8cm | D、12cm |
 如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.
如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.  已知一次函数y=kx+b的图象平行于直线y=-2x+4,且经过点A(2,-2).
已知一次函数y=kx+b的图象平行于直线y=-2x+4,且经过点A(2,-2).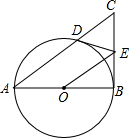 如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边上的动点,连接DE,OE.
如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边上的动点,连接DE,OE. 如图,点A′、B′、C′、D′分别是正方形ABCD四条边上的点,并且AA′=BB′=CC′=DD′,求证:A′C′与B′D′互相垂直且相等.
如图,点A′、B′、C′、D′分别是正方形ABCD四条边上的点,并且AA′=BB′=CC′=DD′,求证:A′C′与B′D′互相垂直且相等.