题目内容
8.把方程2x2-6x+p=0配方,得到(x+m)2=$\frac{1}{2}$.(1)求常数p与m的值;
(2)求此方程的解.
分析 (1)把(x+m)2=$\frac{1}{2}$展开即可得出4m=-6,2m2-1=p,求出即可;
(2)代入后配方得出(x-$\frac{3}{2}$)2=$\frac{1}{2}$,开方得出x-$\frac{3}{2}$=±$\frac{\sqrt{2}}{2}$,求出即可.
解答 解:(1)∵(x+m)2=$\frac{1}{2}$.
∴x2+2mx+m2=$\frac{1}{2}$,
∴x2+2mx+m2-$\frac{1}{2}$=0,
∴2x2+4mx+2m2-1=0,
∴4m=-6,2m2-1=p,
解得:m=-$\frac{3}{2}$,p=$\frac{7}{2}$;
(2)∵2x2-6x+$\frac{7}{2}$=0,
∴x2-3x=-$\frac{7}{4}$,
∴(x-$\frac{3}{2}$)2=$\frac{1}{2}$,
x-$\frac{3}{2}$=±$\frac{\sqrt{2}}{2}$,
即方程的解是:x1=$\frac{3+\sqrt{2}}{2}$,x2=$\frac{3-\sqrt{2}}{2}$.
点评 本题考查了解一元二次方程的应用,题目是一道基础题,难度适中,主要考查学生的计算能力.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
19.点A的坐标为A(2,-4),若点A绕原点逆时针旋转270°后的坐标为( )
| A. | (-4,2) | B. | (-4,-2) | C. | (4,-2) | D. | (4,2) |
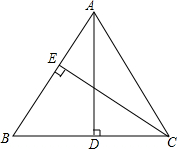 如图,AD,CE分别是△ABC中边BC,AB上的高,若AD=10,CE=9,AB=12,求BC的长.
如图,AD,CE分别是△ABC中边BC,AB上的高,若AD=10,CE=9,AB=12,求BC的长.