题目内容
9.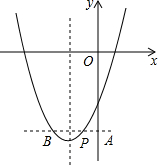 已知抛物线y=x2+(b-1)x+c经过点P(-1,-2b).
已知抛物线y=x2+(b-1)x+c经过点P(-1,-2b).(1)求b+c的值;
(2)如果b=3,求这条抛物线的顶点坐标;
(3)如图所示,过点P作直线PA⊥y轴,交y轴于点A,交抛物线于另一点B,且BP=2PA,求这条抛物线所对应的二次函数关系式.
分析 (1)因为抛物线y=x2+(b-1)x+c经过点P(-1,-2b),所以将点P代入解析式即可求得;
(2)因为b=3,所以求得c的值,即可求得抛物线的解析式,然后利用配方法求出顶点坐标;
(3)根据图形,可得P在对称轴右侧,根据抛物线的对称性以及BP=2PA,可确定点B的坐标;因为点P与点B关于对称轴对称,所以确定对称轴方程,从而求得b、c的值,求得函数解析式.
解答 解:(1)依题意得:(-1)2+(b-1)(-1)+c=-2b,
∴b+c=-2.
(2)当b=3时,c=-5,
∴y=x2+2x-5=(x+1)2-6,
∴抛物线的顶点坐标是(-1,-6). (3)根据图形,可得P在对称轴右侧,
(3)根据图形,可得P在对称轴右侧,
抛物线对称轴为直线x=-$\frac{b-1}{2}$,
∵抛物线是轴对称图形,P(-1,-2b)且BP=2PA,
∴B(-3,-2b),
∴-$\frac{b-1}{2}$=-2,
∴b=5,
又∵b+c=-2,
∴c=-7,
∴抛物线所对应的二次函数关系式为y=x2+4x-7.
点评 此题考查了二次函数图象与系数的关系,待定系数法求函数的解析式,二次函数的对称性,解题的关键是要注意数形结合思想的应用.

练习册系列答案
相关题目
14. 如图,已知正方形铁丝框ABCD边长为10,现使其变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形的面积为( )
如图,已知正方形铁丝框ABCD边长为10,现使其变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形的面积为( )
 如图,已知正方形铁丝框ABCD边长为10,现使其变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形的面积为( )
如图,已知正方形铁丝框ABCD边长为10,现使其变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形的面积为( )| A. | 50 | B. | 100 | C. | 150 | D. | 200 |
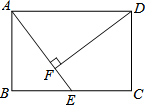 矩形ABCD中,AB=4,AD=6,点E是BC的中点,过点D作DF⊥AE于点F,求cos∠ADF的值.
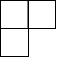
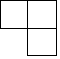
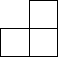
矩形ABCD中,AB=4,AD=6,点E是BC的中点,过点D作DF⊥AE于点F,求cos∠ADF的值.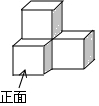 如图是由四个大小相同的正方体组成的几何体,那么它从左面看的形状是( )
如图是由四个大小相同的正方体组成的几何体,那么它从左面看的形状是( )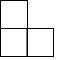
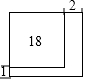 公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长为6m(精确到1m)
公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长为6m(精确到1m) 已知:在?ABCD中,对角线AC⊥BD
已知:在?ABCD中,对角线AC⊥BD 如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点).过点P分别作两坐标轴的垂线,且与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是y=-x+5.
如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点).过点P分别作两坐标轴的垂线,且与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是y=-x+5.