题目内容
4.△ABC中,∠C=90°,BC=3,AB=5,求sinA,cosA,tanA的值.分析 首先利用勾股定理求得AC的长度;然后利用锐角三角函数的定义解答.
解答  解:∵Rt△ABC中,∠C=90°,BC=3,AB=5,
解:∵Rt△ABC中,∠C=90°,BC=3,AB=5,
∴AC=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴sinA=$\frac{BC}{AB}$=$\frac{3}{5}$;
cosA=$\frac{AC}{AB}$=$\frac{4}{5}$;
tanA=$\frac{BC}{AC}$=$\frac{3}{4}$.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
相关题目
9.下列运算中,结果是a18的是( )
| A. | a9+a9 | B. | a3•a6 | C. | (a3)6 | D. | (a2•a3)3 |
16.下列说法中正确的是( )
| A. | 对角线相等的四边形是矩形 | B. | 对角线互相垂直的四边形是正方形 | ||
| C. | 平行四边形的对角线平分一组对角 | D. | 矩形的对角线相等且互相平分 |
14.将一个平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积,则这样的折纸方法共有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 无数种 |

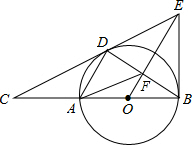 如图,点D是半径为5的⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD,CA=8,过点B作⊙O的切线BE交直线CD于点E,连接AD、BD、OE的交点是F,连接AF.
如图,点D是半径为5的⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD,CA=8,过点B作⊙O的切线BE交直线CD于点E,连接AD、BD、OE的交点是F,连接AF. 某河道A,B两个码头之间有客轮和货轮通行,某天,客轮从A码头出发,匀速行驶到B码头,同时货轮从B码头出发,运送一批建材匀速行驶到A码头.两船距B码头的距离y(千米)与行驶时间x(分钟)之间的函数关系图象如图所示.
某河道A,B两个码头之间有客轮和货轮通行,某天,客轮从A码头出发,匀速行驶到B码头,同时货轮从B码头出发,运送一批建材匀速行驶到A码头.两船距B码头的距离y(千米)与行驶时间x(分钟)之间的函数关系图象如图所示.