题目内容
如图,在△ABC 中,AB=AC,DE 垂直平分 AB,分别交 AB、AC 于点 D、E,若∠EBC=30°, 则∠A=( )
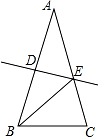
A.30° B.35° C.40° D.45°
C【考点】线段垂直平分线的性质;等腰三角形的性质.
【分析】设∠A 为 x,根据线段的垂直平分线的性质得到 EA=EB,用 x 表示出∠BEC,根据等腰三 角形的性质得到∠ABC=∠C,根据三角形内角和定理列出方程,解方程即可.
【解答】解:设∠A 为 x,
∵DE 垂直平分 AB,
∴EA=EB,
∴∠EBA=∠A=x,
∴∠BEC=2x,
∵AB=AC,
∴∠ABC=∠C,
∴30°+x+30°+2x=180°,
解得,x=40°, 故选:C.
【点评】此题主要考查线段的垂直平分线的性质和三角形内角和定理的应用,掌握线段的垂直平分 线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目


 =_ ___.
=_ ___.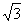 ≈1.732,
≈1.732,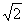 ≈1.414)
≈1.414)