Question

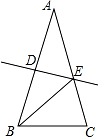
如图，DE^⊥AB 于 E，DF^⊥AC 于 F，若 BD=CD、BE=CF．

（1）求证：AD 平分^∠BAC；

直接写出 AB+AC 与 AE 之间的等量关系．

Answer 1

【考点】角平分线的性质；全等三角形的判定与性质．

【专题】探究型．

【分析】（1）根据相似三角形的判定定理得出^△BDE^≌△CDF，故可得出 DE=DF，所以 AD 平分

^∠BAC；

由（1）中^△BDE^≌△CDE 可知 BE=CF，AD 平分^∠BAC，故可得出^△AED^≌△AFD，所以 AE=AF， 故 AB+AC=AE﹣BE+AF+CF=AE+AE=2AE．

【解答】（1）证明：^∵DE^⊥AB 于 E，DF^⊥AC 于 F，

^∴∠E=^∠DFC=90°，

^∴△BDE  与^△CDE 均为直角三角形，

∵

^∴△BDE^≌△CDF，

^∴DE=DF，即 AD 平分^∠BAC；

AB+AC=2AE．

证明：^∵BE=CF，AD 平分^∠BAC，

^∴∠EAD=^∠CAD，

^∵∠E=^∠AFD=90°，

^∴∠ADE=^∠ADF， 在^△AED 与^△AFD 中，

^∵                           ，

^∴△AED^≌△AFD，

^∴AE=AF，

^∴AB+AC=AE﹣BE+AF+CF=AE+AE=2AE．

【点评】本题考查的是角平分线的性质及全等三角形的判定与性质，熟知角平分线的性质及其逆定 理是解答此题的关键．