题目内容
1.一个三角形的三内角的度数的比为1:1:2,则此三角形( )| A. | 锐角三角形 | B. | 钝角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
分析 设这三个内角度数分别为x、x、2x,根据三角形内角和定理列出方程,解方程即可.
解答 解:设这三个内角度数分别为x、x、2x,则
x+x+2x=180°,
解得x=45°,
∴2x=90°,
∴这个三角形是等腰直角三角形,
故选:D.
点评 本题考查的是三角形内角和定理的应用,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
11.A,B,C三点在⊙O上,OD⊥BC于点D,∠BOD=40°,则∠BAC等于( )
| A. | 20° | B. | 40°或140° | C. | 40° | D. | 20°或160° |
16.数轴上一个点到-5所表示的点的距离为4,那么这个点在数轴上所表示的数是( )
| A. | -2或-8 | B. | -1或-9 | C. | -9 | D. | -1 |
13.已知三角形的两条边长分别为7和3,则第三边的长不能是( )
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
10.若|m|=7,n2=81,且m-n>0,则m+n的值为( )
| A. | 2或16 | B. | -2或-16 | C. | ±2 | D. | ±16 |
11.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
| A. | AB=CD | B. | AD=BC | C. | AB=BC | D. | AC=BD |
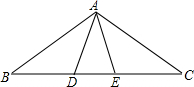 如图,△ABC中,AB=AC,∠B=∠C,点D,E在BC边上,添加一个适当的条件BE=CD时,可以使△ABE≌△ACD.
如图,△ABC中,AB=AC,∠B=∠C,点D,E在BC边上,添加一个适当的条件BE=CD时,可以使△ABE≌△ACD.