题目内容
9. 已知:如图,AB是圆O的直径,CD为弦,连AD、AC,∠CAB=55°,则∠D=( )
已知:如图,AB是圆O的直径,CD为弦,连AD、AC,∠CAB=55°,则∠D=( )| A. | 55° | B. | 50° | C. | 35° | D. | 45° |
分析 由AB为⊙O的直径,根据直径所对的圆周角是直角,∠ACB=90°,又由直角三角形的两锐角互余,即可求得∠B的度数,然后根据在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得答案.
解答 解:∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CAB=55°,
∴∠B=90°-∠CAB=35°,
∴∠ADC=∠B=35°.
故选:C.
点评 此题考查了圆周角定理与直角三角形的性质.此题难度不大,注意直径所对的圆周角是直角与在同圆或等圆中,同弧或等弧所对的圆周角相等定理的应用,注意数形结合思想的应用.

练习册系列答案
相关题目
18.如图由边长相等的黑、白正方形按一定规律拼接而成,依次规律,第8个图形中正方形的个数为( )


| A. | 50 | B. | 51 | C. | 52 | D. | 53 |
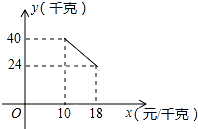 某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示: 二次函数y=ax2+bx+c的图象如图所示,则b2-4ac>0(填“>”“<”或“=”)
二次函数y=ax2+bx+c的图象如图所示,则b2-4ac>0(填“>”“<”或“=”)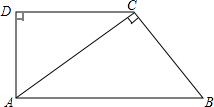 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,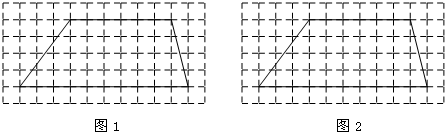
 如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a-b+c的值为0.
如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a-b+c的值为0.