题目内容
把正方形ABCD沿着折痕EF对折，点B恰好落在边CD上的B′点，若AE=2，B′C=3，求正方形ABCD的边长．考点：翻折变换（折叠问题）
专题：
分析：连接BE，B′E，根据轴对称的性质得到BE=B′E．设正方形ABCD的边长为a，则DE=a-2，DB′=a-3，由勾股定理得a2+22=（a-3）2+（a-2）2，解方程求出a的值，即可得到正方形ABCD的边长．
解答：
解：如图，连接BE，B′E．
∵把正方形ABCD沿着折痕EF对折，点B恰好落在边CD上的B′点，
∴BE=B′E．
设正方形ABCD的边长为a，则DE=a-2，DB′=a-3．
在Rt△ABE中，∵∠A=90°，
∴BE2=AB2+AE2=a2+22．
在Rt△DB′E中，∵∠D=90°，
∴B′E2=DB2+DE2=（a-3）2+（a-2）2．
∵BE=B′E，
∴a2+22=（a-3）2+（a-2）2，
整理，得a2-10a+9=0，
解得a1=9，a2=1（不合题意舍去），
故正方形ABCD的边长为9．
解：如图，连接BE，B′E．∵把正方形ABCD沿着折痕EF对折，点B恰好落在边CD上的B′点，
∴BE=B′E．
设正方形ABCD的边长为a，则DE=a-2，DB′=a-3．
在Rt△ABE中，∵∠A=90°，
∴BE2=AB2+AE2=a2+22．
在Rt△DB′E中，∵∠D=90°，
∴B′E2=DB2+DE2=（a-3）2+（a-2）2．
∵BE=B′E，
∴a2+22=（a-3）2+（a-2）2，
整理，得a2-10a+9=0，
解得a1=9，a2=1（不合题意舍去），
故正方形ABCD的边长为9．
点评：本题考查了轴对称的性质，正方形的性质，勾股定理，有一定难度．准确作出辅助线是解题的关键．
练习册系列答案
相关题目
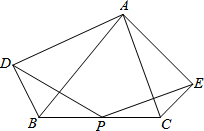如图，点P为△ABC的边BC的中点，分别以AB，AC为斜边作Rt△ABD和Rt△ACE，且∠BAD=∠CAE，求证：PD=PE．
已知：如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．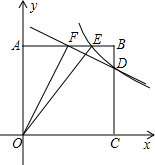
如图，正方形AOCB的边长为4，反比例函数的图象过点E（3，4）．