题目内容
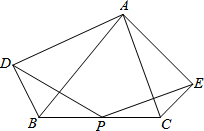 如图,点P为△ABC的边BC的中点,分别以AB,AC为斜边作Rt△ABD和Rt△ACE,且∠BAD=∠CAE,求证:PD=PE.
如图,点P为△ABC的边BC的中点,分别以AB,AC为斜边作Rt△ABD和Rt△ACE,且∠BAD=∠CAE,求证:PD=PE.考点:全等三角形的判定与性质,直角三角形斜边上的中线,三角形中位线定理
专题:证明题
分析:如图,分别取AB、AC的中点M、N,连接DM、PM、PN、NE,构建三角形中位线,利用三角形中位线定理和直角三角形斜边的中线等于斜边的一半证得△MDP≌△NPE(SAS),则该全等三角形的对应边相等:PD=PE.
解答: 证明:如图,分别取AB、AC的中点M、N,连接DM、PM、PN、NE.
证明:如图,分别取AB、AC的中点M、N,连接DM、PM、PN、NE.
∵点P为△ABC的边BC的中点,
∴PM为△ABC的中位线,
∴PM=
AC.
又∵NE为直角△AEC斜边上的中线,
∴NE=AN=
AC,
∴MP=NE.
同理DM=PN.
∵DM=AM,
∴∠1=∠3,
∴∠5=2∠1(三角形外角定理).
同理,∠6=2∠2.
又∠1=∠2,
∴∠5=∠6.
又 PM∥AC,PN∥AB,
∴∠7=∠9,∠8=∠9,
∴∠7=∠8,
∴∠5+∠7=∠6+∠8,即∠DMP=∠PNE,
∴在△MDP与△NPE中,
,
∴△MDP≌△NPE(SAS),
∴PD=PE.
 证明:如图,分别取AB、AC的中点M、N,连接DM、PM、PN、NE.
证明:如图,分别取AB、AC的中点M、N,连接DM、PM、PN、NE.∵点P为△ABC的边BC的中点,
∴PM为△ABC的中位线,
∴PM=
| 1 |
| 2 |
又∵NE为直角△AEC斜边上的中线,
∴NE=AN=
| 1 |
| 2 |
∴MP=NE.
同理DM=PN.
∵DM=AM,
∴∠1=∠3,
∴∠5=2∠1(三角形外角定理).
同理,∠6=2∠2.
又∠1=∠2,
∴∠5=∠6.
又 PM∥AC,PN∥AB,
∴∠7=∠9,∠8=∠9,
∴∠7=∠8,
∴∠5+∠7=∠6+∠8,即∠DMP=∠PNE,
∴在△MDP与△NPE中,
|
∴△MDP≌△NPE(SAS),
∴PD=PE.
点评:本题考查了全等三角形的判定与性质,直角三角形斜边上的中线以及三角形中位线定理.根据题意作出辅助线是解题的难点,也是解题的关键.

练习册系列答案
相关题目
元旦节日期间,某商场为了促销,每件夹克按成本价提高50%后标价,后因季节关系按标价的8折出售,每件以168元卖出,这批夹克每件的成本价是( )
| A、80元 | B、84元 |
| C、140元 | D、100元 |


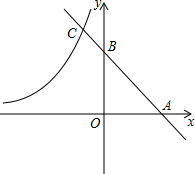 如图,直线y=-x+m与双曲线y=-
如图,直线y=-x+m与双曲线y=- 把正方形ABCD沿着折痕EF对折,点B恰好落在边CD上的B′点,若AE=2,B′C=3,求正方形ABCD的边长.
把正方形ABCD沿着折痕EF对折,点B恰好落在边CD上的B′点,若AE=2,B′C=3,求正方形ABCD的边长.