题目内容
4.(1)引入:如图1,直线AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC,直线BC是否与⊙O相切,为什么?
(2)引申:
如图2,记(1)中⊙O的切线为直线l,在(1)的条件下,将切线l向下平移,设平移后的直线l与OB的延长线相交于点B′,与AB的延长线相交于点E,与OP的延长线相交于点C′,找出图2中与C′P相等的线段,并说明理由.
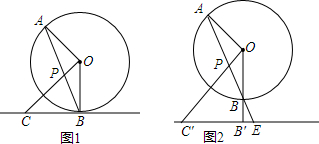
分析 (1)由OC⊥OA,易得∠APO+∠OAB=90°,由等腰三角形的性质可得∠OAB=∠ABO,∠CBP=∠CPB,等量代换可得∠CBP+∠OBA=90°,即∠OBC=90°,由切线的判定定理得出结论;
(2)由(1)可得∠OAB+∠C′PE=90°,等量代换可得∠ABO+∠C′PE=90°,由∠EBB′+∠BEB′=90°,∠EBB′=∠ABO,易得∠C′PE=∠BEB′,得出C′P=C′E.
解答 解:(1)相切,
∵OC⊥OA,∴∠AOC=90°,
∴∠APO+∠OAB=90°,
∵OA=OB,∴∠OAB=∠ABO,
∵PC=PB,∴∠CBP=∠CPB,
∵∠APO=∠CPB,
∴∠CBP+∠OBA=90°,即∠OBC=90°,
∴OB⊥BC
∵OB为半径,
∴BC与⊙O相切;
(2)C′P=C′E,
∵∠OB′C′=90°,∠APO+∠OAB=90°,且∠APO=∠C′PE,
∴∠OAB+∠C′PE=90°,
∵OA=OB,
∴∠OAB=∠ABO,
∴∠ABO+∠C′PE=90°,
∵∠EBB′+∠BEB′=90°,且∠EBB′=∠ABO,
∴∠C′PE=∠BEB′,
∴C′P=C′E.
点评 本题主要考查了等腰三角形的性质及判定和切线的判定定理,利用等腰三角形的性质和等量代换是解答此题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
12.一个盒子有1个红球,1个白球,这两个球除颜色外其余都相同,从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,则两次都摸出红球的概率为( )
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
9.一个两位数,十位上的数字是a,个位上的数字是b,则交换十位数字与个位数字之后,所得的新的两位数为( )
| A. | a+b | B. | ab | C. | 10a+b | D. | 10b+a |
 已知:如图,BE∥DF,AE=CF,∠A=∠C,求证:AB=CD.
已知:如图,BE∥DF,AE=CF,∠A=∠C,求证:AB=CD.