题目内容
等边三角形ABC中,BC=6,D、E是边BC上两点,且BD=CE=1,点P是线段DE上的一个动点,过点P分别作AC、AB的平行线交AB、AC于点M、N,连接MN、AP交于点G,则点P由点D移动到点E的过程中,线段BG扫过的区域面积为 .


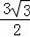
 .
.
【考点】轨迹.
【分析】求出四边形AMPN是平行四边形,根据平行四边形的对角线互相平分可得G是AP的中点,然后判断出点G的运动路线是△APP′的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半求出GG′,再根据等边三角形的性质求出△BGG′的底边GG′上的高,然后根据三角形的面积公式列式计算即可得解.
【解答】解:∵PM∥AC,PN∥AB,
∴四边形AMPN是平行四边形,
∵MN与AP相交于点G,
∴G是AP的中点,
∴如图点G的运动路线是△APP′的中位线,
∵BC=6,BD=CE=1,
∴GG′=
 =2,
=2,
∵BC=6,
∴△BGG′的底边GG′上的高=
 ×(6×
×(6×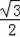
 )=
)=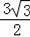
 ,
,
∴线段BG扫过的区域面积=
 ×2×
×2×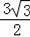
 =
=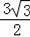
 .
.
故答案为: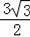
 .
.
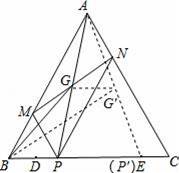

【点评】本题考查了点的轨迹,等边三角形的性质,平行四边形的判定与性质,三角形的中位线平行于第三边并且等于第三边的一半,难点在于确定出点G的运动轨迹从而确定出BG扫过的区域是三角形.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 .
.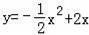
 上,则下列结论正确的是( )
上,则下列结论正确的是( )



 的图象上;
的图象上;