��Ŀ����
��ͼ1��ƽ��ֱ������ϵ�У�����ֱ�������ε�ֱ�DZ�BC��x���������ϻ�������C������Ϊ��t��0����ֱ�DZ�AC=4������O��C������������y1=ax��x��t����aΪ������a��0��������������б��AB���ڵ�E��ֱ��OA��y2=kx��kΪ������k��0��
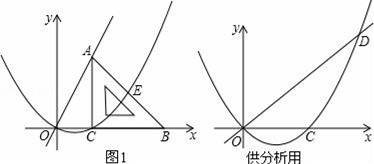

��1����գ��ú�t�Ĵ���ʽ��ʾ��A�����꼰k��ֵ��A��������������k=��������������
��2���������ǰ�Ļ�������a=
 ʱ��
ʱ��
��������֤��������y1=ax��x��t���Ķ����ں���y=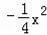
 ��ͼ���ϣ�
��ͼ���ϣ�
�ڵ����ǰ廬����EΪAB���е�ʱ����t��ֵ��
��3��ֱ��OA�������ߵ���һ������Ϊ��D����t��x��t+4��|y2��y1|��ֵ��x���������С����x��t+4ʱ��|y2��y1|��ֵ��x�������������a��t�Ĺ�ϵʽ��t��ȡֵ��Χ��
�����㡿���κ����ۺ��⣮
��ר�⡿ѹ���⣮
����������1�����������õ�A�ĺ��������C����ͬ����A�������꼴���߶�AC�ij��ȣ��ѵ�A���������ֱ��OA�Ľ���ʽ����k��ֵ��
��2�������������y1�Ķ������꣬Ȼ��Ѹ�������뺯��y=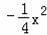
 �����õ����㺯������ʽy=
�����õ����㺯������ʽy=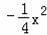
 ������ʾ�ö����ں���y=
������ʾ�ö����ں���y=
 ͼ���ϣ���֮���ö��㲻�ں���y=
ͼ���ϣ���֮���ö��㲻�ں���y=
 ͼ���ϣ�
ͼ���ϣ�
����ͼ1������E��EK��x���ڵ�K����EK�ǡ�ACB����λ�ߣ����Ը�����������λ�߶��������E�����꣬�ѵ�E���������������y1=
 x��x��t���������t=2��
x��x��t���������t=2��
��3����ͼ2��������������ֱ���ཻ������õ�D��������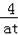
 +4����t+4=
+4����t+4=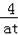
 +4���ɴ˿������a��t�Ĺ�ϵʽ��
+4���ɴ˿������a��t�Ĺ�ϵʽ��
����𡿽⣺��1���ߵ�C������Ϊ��t��0����ֱ�DZ�AC=4��
���A�������ǣ�t��4����
�֡�ֱ��OA��y2=kx��kΪ������k��0����
��4=kt����k=
 ��k��0����
��k��0����
��2���ٵ�a=
 ʱ��y1=
ʱ��y1=
 x��x��t�����䶥������Ϊ��
x��x��t�����䶥������Ϊ��
 ����
����
 ����
����
����y=
 ��˵����x=
��˵����x=
 ʱ��y=
ʱ��y=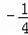
 ��
��
 =��
=��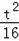
 �����㣨
�����㣨
 ����
����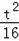
 ����������y=
����������y=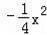
 �ϣ�
�ϣ�
�ʵ�a=
 ʱ��������y1=ax��x��t���Ķ����ں���y=
ʱ��������y1=ax��x��t���Ķ����ں���y=
 ��ͼ���ϣ�
��ͼ���ϣ�
����ͼ1������E��EK��x���ڵ�K��
��AC��x�ᣬ
��AC��EK��
�ߵ�E���߶�AB���е㣬
��KΪBC���е㣬
��EK�ǡ�ACB����λ�ߣ�
��EK=
 AC=2��CK=
AC=2��CK=
 BC=2��
BC=2��
��E��t+2��2����
�ߵ�E��������y1=
 x��x��t���ϣ�
x��x��t���ϣ�
��
 ��t+2����t+2��t��=2��
��t+2����t+2��t��=2��
���t=2��
��3����ͼ2��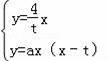
 ����
����
 x=ax��x��t����
x=ax��x��t����
���x=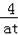
 +t����x=0���������⣬��ȥ����
+t����x=0���������⣬��ȥ����
�ʵ�D�ĺ�������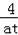
 +t��
+t��
��x=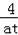
 +tʱ��|y2��y1|=0���������t+4=
+tʱ��|y2��y1|=0���������t+4=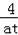
 +t��
+t��
��at=1��
��y2��y1=
 x��ax��x��t��=��ax2+��at+
x��ax��x��t��=��ax2+��at+
 ��x=��a[x2����t+
��x=��a[x2����t+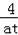
 ��x+��
��x+��
 +
+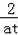
 ��2]+a��
��2]+a��
 +
+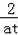
 ��2
��2
=��a[x����
 +
+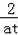
 ��]2+a��
��]2+a��
 +
+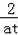
 ��2
��2
�൱x=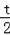
 +
+
 ʱ��y2��y1ȡ�����ֵ��
ʱ��y2��y1ȡ�����ֵ��
�֡ߵ�x=
 +tʱ��|y2��y1|=0��
+tʱ��|y2��y1|=0��
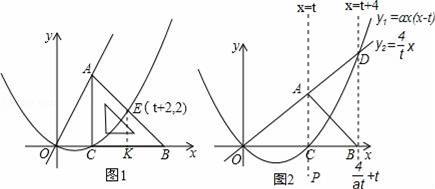
�൱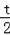
 +
+
 ��x��
��x��
 +tʱ��|y2��y1|��x���������С����x��
+tʱ��|y2��y1|��x���������С����x��
 +tʱ��|y2��y1|��x�����������
+tʱ��|y2��y1|��x�����������
����������Ҫ���㵱t��x��t+4��|y2��y1|��ֵ��x���������С����x��t+4ʱ��|y2��y1|��ֵ��x�����������
��t��
 +
+
 ������������
������������
��at=1��
����t��4��
����������a��t�Ĺ�ϵʽ��t��ȡֵ��ΧΪat=1��t��4����

�����������⿼����������ͼ�ε����ʡ����κ���ͼ���ϵ������������һ�κ�������κ������������֪ʶ�㣮����ʱ��ע�⡰���ν�ϡ���ѧ˼���Ӧ�ã�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�






 B��
B��



 +
+
 +3����
+3����
 =��������������
=�������������� B��
B�� C��
C�� D��
D��