题目内容
11.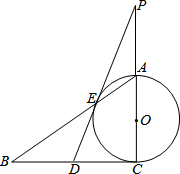 如图,Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点E,D是BC的中点,DE的延长线交CA的延长线于点P.
如图,Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点E,D是BC的中点,DE的延长线交CA的延长线于点P.(1)求证:DE是⊙O的切线;
(2)若sin∠P=$\frac{1}{3}$,PC=8,求⊙O的直径;
(3)若$\frac{PE}{PD}=\frac{2}{3}$,求cos∠BAC值.
分析 (1)连结OE,CE,求出DE=$\frac{1}{2}$BC=DC,推出∴∠DEC+∠OEC=∠DCE+∠OCE,求出∠ACB=∠OED=90°,根据切线的判定推出即可.
(2)在RT△POE中,由sin∠P=$\frac{OE}{PO}$=$\frac{1}{3}$,得出PO=3OE,设圆的半径为R,根据PC=8,得出4R=8,从而求得R=2,即可求得⊙O的直径为4.
(3)作EF⊥AC于F,得出EF∥BC,根据平行线分线段成比例定理得出$\frac{EF}{DC}$=$\frac{PE}{PD}$=$\frac{2}{3}$,求得$\frac{EF}{BC}$=$\frac{1}{3}$,根据EF∥BC,得出$\frac{AF}{AC}$=$\frac{EF}{BC}$=$\frac{1}{3}$,从而求得AF=$\frac{2}{3}$R,OF=$\frac{1}{3}$R,然后根据勾股定理AE=$\frac{2\sqrt{3}}{3}$R,根据直角三角形的余弦函数从而求得cos∠BAC=$\frac{AF}{AE}$=$\frac{\sqrt{3}}{3}$.
解答 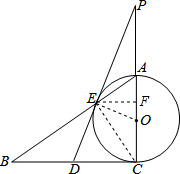 (1)证明:连结OE,CE,
(1)证明:连结OE,CE,
∵AC是直径,
∴∠AEC=90°,
∴∠BEC=90°,
∵D是BC的中点,
∴DE=$\frac{1}{2}$BC=DC,
∴∠DEC=∠DCE.
∵OC=OE,
∴∠OEC=∠OCE,
∴∠DEC+∠OEC=∠DCE+∠OCE,
即∠ACB=∠OED,
∵∠ACB=90°,
∴∠OED=90°,
又∵OD是半径,
∴DE是⊙O的切线.
(2)解:在RT△POE中,sin∠P=$\frac{OE}{PO}$=$\frac{1}{3}$,
∴PO=3OE,
设圆的半径为R,
∵PC=8,
∴4R=8,
∴R=2,
∴⊙O的直径为4.
(3)解:作EF⊥AC于F,
∴EF∥BC,
∴$\frac{EF}{DC}$=$\frac{PE}{PD}$=$\frac{2}{3}$,
∵BC=2DC,
∴$\frac{EF}{BC}$=$\frac{1}{3}$,
∵EF∥BC,
∴$\frac{AF}{AC}$=$\frac{EF}{BC}$=$\frac{1}{3}$,
∵AC=2R,
∴AF=$\frac{2}{3}$R,
∴OF=R-$\frac{2}{3}$R=$\frac{1}{3}$R,
∴EF2=OE2-OF2=R2-($\frac{1}{3}$R)2=$\frac{8}{9}$R2
∴AE=$\sqrt{E{F}^{2}+A{F}^{2}}$=$\sqrt{{\frac{8}{9}R}^{2}+(\frac{2}{3}R)^{2}}$=$\frac{2\sqrt{3}}{3}$R,
∴cos∠BAC=$\frac{AF}{AE}$=$\frac{\frac{2}{3}R}{\frac{2\sqrt{3}}{3}R}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了切线的判定,圆周角定理的应用,平行线分线段成比例定理的应用,勾股定理的应用等,熟练掌握性质定理是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | (3,4) | B. | (-3,4) | C. | (-3,-4) | D. | (4,3) |
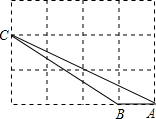 如图,△ABC的三个顶点都在方格纸的格点上,则sinA=( )
如图,△ABC的三个顶点都在方格纸的格点上,则sinA=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{5}}{5}$ |
 如图,在山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100米,则山高AB=50$\sqrt{3}$+50米.
如图,在山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100米,则山高AB=50$\sqrt{3}$+50米. 如图所示,已知OB⊥OA,直线CD过点O,且∠AOC=35°,则∠BOD=125°.
如图所示,已知OB⊥OA,直线CD过点O,且∠AOC=35°,则∠BOD=125°.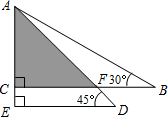 将一副三角尺按如图所示叠放在一起,若AB=12cm,则阴影部分的面积是18cm2.
将一副三角尺按如图所示叠放在一起,若AB=12cm,则阴影部分的面积是18cm2.