题目内容
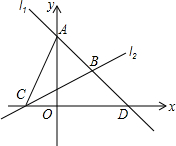 如图,一次函数y=kx+b的图象为直线l1,经过A(0,4)和D(4,0)两点;一次函数y=
如图,一次函数y=kx+b的图象为直线l1,经过A(0,4)和D(4,0)两点;一次函数y=| 1 |
| 2 |
(1)求k、b的值;
(2)求点B的坐标;
(3)求△ABC的面积.
考点:两条直线相交或平行问题
专题:计算题
分析:(1)把点A和点D的坐标分别代入y=kx+b得到关于k、b的方程组,然后解方程求出k、b的值;
(2)根据两直线相交的问题,通过解方程组
得到点B的坐标;
(3)先确定C点坐标,然后利用△ABC的面积=S△ACD-S△BCD进行计算.
(2)根据两直线相交的问题,通过解方程组
|
(3)先确定C点坐标,然后利用△ABC的面积=S△ACD-S△BCD进行计算.
解答:解:(1)把A(0,4)和D(4,0)分别代入y=kx+b得
,解得
;
(2)解方程组
得
,
所以点B的坐标为(2,2);
(3)当y=0时,
x+1=0,解得x=-2,则C点坐标为(-2,0),
所以△ABC的面积=S△ACD-S△BCD
=
×(4+2)×4-
×(4+2)×2
=6.
|
|
(2)解方程组
|
|
所以点B的坐标为(2,2);
(3)当y=0时,
| 1 |
| 2 |
所以△ABC的面积=S△ACD-S△BCD
=
| 1 |
| 2 |
| 1 |
| 2 |
=6.
点评:本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC.若∠A=36°,则∠C的度数为( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC.若∠A=36°,则∠C的度数为( )| A、18° | B、27° |
| C、36° | D、54° |
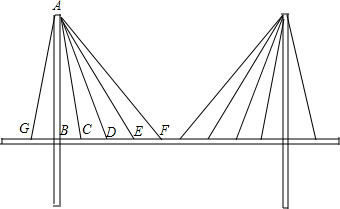 二次根式的加减在日常生活中有着广泛的应用.如在一座斜拉桥上可以看到很多拉索.如图所示,事实上,AB⊥GF.若AB=24m,BC=2m,BC=CD=DE=EF,桥的两个立柱两边各拉4条这样的拉索,那么拉索的总长度是多少米?
二次根式的加减在日常生活中有着广泛的应用.如在一座斜拉桥上可以看到很多拉索.如图所示,事实上,AB⊥GF.若AB=24m,BC=2m,BC=CD=DE=EF,桥的两个立柱两边各拉4条这样的拉索,那么拉索的总长度是多少米?