题目内容
如图，在边长为4的正方形ABCD中，动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动，动点F以每秒2个单位长度的速度从点B开始沿折线BC-CD向点D运动，动点E比动点F先出发1秒，其中一个动点到达终点时，另一个动点也随之停止运动，设点F的运动时间为t秒．
（1）点F在边BC上．
①如图1，连接DE，AF，若DE⊥AF，求t的值；
②如图2，连结EF，DF，当t为何值时，△EBF与△DCF相似？
（2）如图3，若点G是边AD的中点，BG，EF相交于点O，试探究：是否存在在某一时刻t，使得
=
？若存在，求出t的值；若不存在，请说明理由．
（1）点F在边BC上．
①如图1，连接DE，AF，若DE⊥AF，求t的值；
②如图2，连结EF，DF，当t为何值时，△EBF与△DCF相似？
（2）如图3，若点G是边AD的中点，BG，EF相交于点O，试探究：是否存在在某一时刻t，使得
| BO |
| OG |
| 1 |
| 6 |
考点：四边形综合题
专题：几何综合题
分析：（1）①利用正方形的性质及条件，得出△ABF≌△DAE，由AE=BF列式计算．
②利用△EBF∽△DCF，得出
=
，列出方程求解．
（2）①0＜t≤2时如图3，以点B为原点，BC为x轴，BA为y轴建立坐标系，先求出EF所在的直线和BG所在的直线函数关系式，再利用勾股定理求出BG，运用
=
，求出点O的坐标，把O的坐标代入EF所在的直线函数关系式求解．②当t＞2时如图4，以点B为原点，BC为x轴，BA为y轴建立坐标系，先求出EF所在的直线和BG所在的直线函数关系式，再利用勾股定理求出BG，运用
=
，求出点O的坐标，把O的坐标代入EF所在的直线函数关系式求解．
②利用△EBF∽△DCF，得出
| EB |
| DC |
| BF |
| FC |
（2）①0＜t≤2时如图3，以点B为原点，BC为x轴，BA为y轴建立坐标系，先求出EF所在的直线和BG所在的直线函数关系式，再利用勾股定理求出BG，运用
| BO |
| OG |
| 1 |
| 6 |
| BO |
| OG |
| 1 |
| 6 |
解答：解：（1）①如图1
∵DE⊥AF，
∴∠AOE=90°，
∴∠BAF+∠AEO=90°，
∵∠ADE+∠AEO=90°，
∴∠BAF=∠ADE，
又∵四边形ABCD是正方形，
∴AB=AD，∠ABF=∠DAE=90°，
在△ABF和△DAE中，
，
∴△ABF≌△DAE（ASA）
∴AE=BF，
∴1+t=2t，
解得t=1．
②如图2，
∵四边形ABCD是正方形，
∴AB=BC=CD=4，
∵BF=2t，AE=1+t，
∴FC=4-2t，BE=4-1-t=3-t，
当△EBF∽△DCF时，
=
，
∴
=
，
解得，t=
，t=
（舍去），
故t=
．
当△EBF∽△FCD时，
=
，
∴
=
，
∴t2-3t+3=0，方程没有实数根，
所以当t=
时，△EBF与△DCF相似；
（2）①0＜t≤2时，如图3，以点B为原点，BC为x轴，BA为y轴建立坐标系，
A的坐标（0，4），G的坐标（2，4），F点的坐标（2t，0），E的坐标（0，3-t）
EF所在的直线函数关系式是：y=
x+3-t，
BG所在的直线函数关系式是：y=2x，
∵BG=
=2
∵
=
，
∴BO=
，OG=
，
设O的坐标为（a，b），
解得
∴O的坐标为（
，
）
把O的坐标为（
，
）代入y=
x+3-t，得
=
×
+3-t，
解得，t=
（舍去），t=
，
②当3≥t＞2时如图4，以点B为原点BC为x轴，BA为y轴建立坐标系，
A的坐标（0，4），G的坐标（2，4），F点的坐标（4，2t-4），E的坐标（0，3-t），
EF所在的直线函数关系式是：y=
x+3-t，
BG所在的直线函数关系式是：y=2x，
∵BG=
=2
∵
=
，
∴BO=
，OG=
，
设O的坐标为（a，b），
解得
∴O的坐标为（
，
）
把O的坐标为（
，
）代入y=
x+3-t，得
=
×
+3-t，
解得：t=
．
综上所述，存在t=
或t=
，使得
=
．
∵DE⊥AF，∴∠AOE=90°，
∴∠BAF+∠AEO=90°，
∵∠ADE+∠AEO=90°，
∴∠BAF=∠ADE，
又∵四边形ABCD是正方形，
∴AB=AD，∠ABF=∠DAE=90°，
在△ABF和△DAE中，
|
∴△ABF≌△DAE（ASA）
∴AE=BF，
∴1+t=2t，
解得t=1．
②如图2，
∵四边形ABCD是正方形，
∴AB=BC=CD=4，
∵BF=2t，AE=1+t，
∴FC=4-2t，BE=4-1-t=3-t，
当△EBF∽△DCF时，| EB |
| DC |
| BF |
| FC |
∴
| 3-t |
| 4 |
| 2t |
| 4-2t |
解得，t=
9-
| ||
| 2 |
9+
| ||
| 2 |
故t=
9-
| ||
| 2 |
当△EBF∽△FCD时，
| BE |
| FC |
| BF |
| CD |
∴
| 3-t |
| 4-2t |
| 2t |
| 4 |
∴t2-3t+3=0，方程没有实数根，
所以当t=
9-
| ||
| 2 |
（2）①0＜t≤2时，如图3，以点B为原点，BC为x轴，BA为y轴建立坐标系，
A的坐标（0，4），G的坐标（2，4），F点的坐标（2t，0），E的坐标（0，3-t）
EF所在的直线函数关系式是：y=
| t-3 |
| 2t |
BG所在的直线函数关系式是：y=2x，
∵BG=
| 22+42 |
| 5 |
∵
| BO |
| OG |
| 1 |
| 6 |
∴BO=
2
| ||
| 7 |
12
| ||
| 7 |
设O的坐标为（a，b），
|
解得
|
∴O的坐标为（
| 2 |
| 7 |
| 4 |
| 7 |
把O的坐标为（
| 2 |
| 7 |
| 4 |
| 7 |
| t-3 |
| 2t |
| 4 |
| 7 |
| t-3 |
| 2t |
| 2 |
| 7 |
解得，t=
9+2
| ||
| 7 |
9-2
| ||
| 7 |
②当3≥t＞2时如图4，以点B为原点BC为x轴，BA为y轴建立坐标系，
A的坐标（0，4），G的坐标（2，4），F点的坐标（4，2t-4），E的坐标（0，3-t），
EF所在的直线函数关系式是：y=
| 3t-7 |
| 4 |
BG所在的直线函数关系式是：y=2x，
∵BG=
| 22+42 |
| 5 |
∵
| BO |
| OG |
| 1 |
| 6 |
∴BO=
2
| ||
| 7 |
12
| ||
| 7 |
设O的坐标为（a，b），
|
解得
|
∴O的坐标为（
| 2 |
| 7 |
| 4 |
| 7 |
把O的坐标为（
| 2 |
| 7 |
| 4 |
| 7 |
| 3t-7 |
| 4 |
| 4 |
| 7 |
| 3t-7 |
| 4 |
| 2 |
| 7 |
解得：t=
| 27 |
| 11 |
综上所述，存在t=
9-2
| ||
| 7 |
| 27 |
| 11 |
| BO |
| OG |
| 1 |
| 6 |
点评：本题主要考查了四边形的综合题，解题的关键是把四边形与坐标系相结合求解．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如果关于x的方程x2-x+k=0（k为常数）有两个不相等的实数根，则k的取值范围是（ ）
A、k＜
| ||
B、k＞
| ||
| C、k＜4 | ||
| D、k＞3 |
如图，△ABC和△DEF的边BC、EF重叠的部分为FC，有下列四个条件：①AB=DE，②BF=EC，③∠B=∠E，④∠ACB=∠DFE．请你从这四个条件中选出三个作为题设，另一个作为结论，组成一个真命题，并给予证明．题设：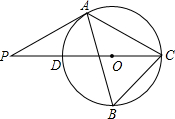
如图，△ABC内接于⊙O，∠B=60°，CD是⊙O的直径，点P是CD延长线上的一点，PA是⊙O的切线；
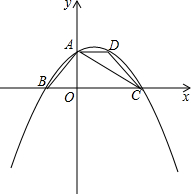如图，在平面直角坐标系中，四边形ABCD是等腰梯形，AD∥BC，AB=DC，BC在x轴上，点A在y轴的正半轴上，点A，D的坐标分别为A（0，2），D（2，2），AB=2
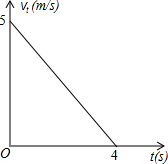一个小球以初始速度v0=5m/s运动，并且均匀减速，4s后停止运动，下图是运动时间t（s）与第t秒末的速度vt（m/s）的函数图象，下表是小球t秒内所走的路与时间的一些数据：