题目内容
13. 如图,⊙O中,AB、CD是⊙O的直径,F是⊙O上一点,连接BC、BF,若点B是弧CF的中点.
如图,⊙O中,AB、CD是⊙O的直径,F是⊙O上一点,连接BC、BF,若点B是弧CF的中点.(1)求证:△ABF≌△DCB;
(2)若CD⊥AF,垂足为E,AB=10,∠C=60°,求EF的长.
分析 (1)根据点B是弧CF的中点,得BF=BC,根据HL即可得出△ABF≌△DCB;
(2)易得BC=5,则BF=5,在Rt△ABF中,根据勾股定理得出AF,根据CD⊥AF,得出EF的值即可.
解答 证明:(1)∵AB、CD是⊙O的直径,
∴AB=CD,∠F=∠CBD=90°,
点B是弧CF的中点,
∴BF=BC,
在Rt△ABF≌Rt△DCB中,
$\left\{\begin{array}{l}{AB=CD}\\{BF=BC}\end{array}\right.$,
∴Rt△ABF≌Rt△DCB(HL),
(2)∵∠C=60°,
∴∠ABF=60°,
∴∠A=30°,
∴BF=$\frac{1}{2}$AB,
∵AB=10,
∴BF=5,
在Rt△ABF中,AF=$\sqrt{A{B}^{2}-B{F}^{2}}$=5$\sqrt{3}$,
∵CD⊥AF,
∴EF=$\frac{1}{2}$AF=$\frac{5}{2}$$\sqrt{3}$.
点评 本题考查了勾股定理,圆周角定理,垂径定理,等知识点的应用,关键是熟练地运用定理进行推理和计算,题型较好,综合性比较强,但难度不大.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
8.根据下列表格中的数值,判断方程ax2+bx+c=0(a,b为常数)根的情况( )
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| ax2+bx+c | … | -3 | 2 | 3 | 0 | -7 | … |
| A. | 有两个不相等实根 | B. | 有两个相等实根 | ||
| C. | 只有一个实根 | D. | 无实根 |
3.计算$\sqrt{36}$的结果是( )
| A. | 6 | B. | ±6 | C. | -6 | D. | 36 |
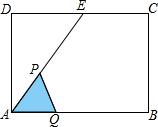 如图,在矩形ABCD中,AB=4cm,AD=2$\sqrt{3}$cm,E为CD边上的中点,点P从点A沿AE运动到点E,点Q从点A沿AB运动到点B时,它们运动的速度都是1cm/s.如果点P,Q同时开始运动,设运动时间为t(s),△APQ的面积为y(cm2),则y与t的函数关系式是y=$\frac{\sqrt{3}}{4}$t2(0<t≤4).
如图,在矩形ABCD中,AB=4cm,AD=2$\sqrt{3}$cm,E为CD边上的中点,点P从点A沿AE运动到点E,点Q从点A沿AB运动到点B时,它们运动的速度都是1cm/s.如果点P,Q同时开始运动,设运动时间为t(s),△APQ的面积为y(cm2),则y与t的函数关系式是y=$\frac{\sqrt{3}}{4}$t2(0<t≤4). 如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周)
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周)