题目内容
10.已知抛物线y=ax2-2x+1与x轴有两个交点,那么a的取值范围是( )| A. | a<1且a≠0 | B. | a>1且a≠2 | C. | a≥1且a≠2 | D. | a≤1且a≠0 |
分析 根据题意,令y=0,得方程ax2-2x+1=0,有两个不同的根得△>0,从而解出a的范围.
解答 解:∵抛物线y=ax2-2x+1与x轴有两个交点,
∴a≠0,△>0,
∴4-4a×1>0,
∴a<1,
故答案为:a<1且a≠0.
故选A.
点评 此题主要考查一元二次方程与函数的关系,关键是理解函数与x轴的交点的横坐标就是方程的根,若方程有根说明函数与x轴有交点,两者互相转化,要充分运用这一点来解题.

练习册系列答案
相关题目
5.已知:x-2y=-3,则代数式(2y-x)2-2x+4y-1的值为( )
| A. | 2 | B. | 14 | C. | -4 | D. | 0 |
19. 如图,在正方形网格中有四个三角形,其中与△ABC相似(不包括△ABC本身)的三角形有( )
如图,在正方形网格中有四个三角形,其中与△ABC相似(不包括△ABC本身)的三角形有( )
 如图,在正方形网格中有四个三角形,其中与△ABC相似(不包括△ABC本身)的三角形有( )
如图,在正方形网格中有四个三角形,其中与△ABC相似(不包括△ABC本身)的三角形有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
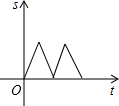
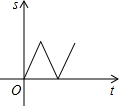
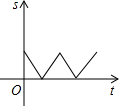
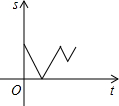
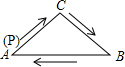 如图,在△ABC中,AC=BC,有一动点P从A出发,沿A→C→B→A匀速运动.设点P的运动时间为t,CP的长度s,则s与t之间的函数关系用图象描述大致是( )
如图,在△ABC中,AC=BC,有一动点P从A出发,沿A→C→B→A匀速运动.设点P的运动时间为t,CP的长度s,则s与t之间的函数关系用图象描述大致是( )