题目内容
3.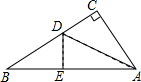 如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
分析 首先由勾股定理求得AB=10,然后由翻折的性质求得BE=4,设DC=x,则BD=8-x,在△BDE中,利用勾股定理列方程求解即可.
解答 解:在Rt△ABC中,由勾股定理可知:AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10,
由折叠的性质可知:DC=DE,AC=AE=6,∠DEA=∠C=90°,
∴BE=AB-AE=10-6=4,∠DEB=90°,
设DC=x,则BD=8-x,DE=x,
在Rt△BED中,由勾股定理得:BE2+DE2=BD2,
即42+x2=(8-x)2,
解得:x=3,
∴CD=3.
故选A.
点评 本题主要考查的是翻折变换、勾股定理的应用;熟练掌握翻折的性质和勾股定理是解决问题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
18.下列真命题中,逆命题也是真命题的是( )
| A. | 全等三角形的对应角都相等 | |
| B. | 如果两个实数相等,那么这两个实数的平方相等 | |
| C. | 对顶角相等 | |
| D. | 等边三角形每一个都等于60° |
15.3°=( )
| A. | 180′ | B. | 18′ | C. | 30′ | D. | 3′ |
12.我市某草莓种植农户喜获丰收,共收获草莓2000kg.经市场调查,可采用批发、零售两种销售方式,这两种销售方式每kg草莓的利润如下表:
设按计划全部售出后的总利润为y元,其中批发量为xkg.
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该农户按计划全部售完后获得的最大利润.
| 销售方式 | 批发 | 零售 |
| 利润(元/kg) | 6 | 12 |
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该农户按计划全部售完后获得的最大利润.
 如图所示,已知二次函数经过点B(3,0),C(0,3),D(4,-5)
如图所示,已知二次函数经过点B(3,0),C(0,3),D(4,-5) 如图,点C在线段AB上,AC=3,BC=5,点M是AC的中点,点N是BC的中点,求线段MN的长度.
如图,点C在线段AB上,AC=3,BC=5,点M是AC的中点,点N是BC的中点,求线段MN的长度. 如图,在边长为2$\sqrt{3}$的正方形ABCD中,点E为AD边的中点,将△ABE沿BE翻折,使点A落在点A′处,作射线EA′,交BC的延长线于点F,则CF=$\frac{\sqrt{3}}{2}$.
如图,在边长为2$\sqrt{3}$的正方形ABCD中,点E为AD边的中点,将△ABE沿BE翻折,使点A落在点A′处,作射线EA′,交BC的延长线于点F,则CF=$\frac{\sqrt{3}}{2}$.