题目内容
8.先化简,再求代数式$\frac{{x}^{2}}{{x}^{2}+4x+4}$÷$\frac{x}{x+2}$-$\frac{x-1}{x+2}$的值,其中x=$\sqrt{2}$-2.分析 先把分母因式分解和除法化为乘法运算,再约分,然后进行同分母的减法运算,最后把x的值代入计算即可.
解答 解:原式=$\frac{{x}^{2}}{(x+2)^{2}}$•$\frac{x+2}{x}$-$\frac{x-1}{x+2}$
=$\frac{x}{x+2}$-$\frac{x-1}{x+2}$
=$\frac{x-x+1}{x+2}$
=$\frac{1}{x+2}$,
当x=$\sqrt{2}$-2时,原式=$\frac{1}{\sqrt{2}-2+2}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
18.线段CD是由线段AB平移得到的,点A(-1,4)的对应点为C(-1,7),则点B(-4,-1)的对应点D的坐标为( )
| A. | (2,9) | B. | (5,3) | C. | (-4,2) | D. | (-9,-4) |
3.抛物线y=-x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
从上表可知,有下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是$\frac{5}{2}$;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是$\frac{5}{2}$;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
| A. | ①②③ | B. | ②③④ | C. | ②③ | D. | ①④ |
13.若函数y=$\frac{m-2}{x}$的图象在其所在的每一个象限内,函数值y随自变量x的增大而增大,则m的取值范围是( )
| A. | m<2 | B. | m<0 | C. | m>2 | D. | m>0 |
17. 如图,点B、C在∠DAE的边上,AB=AC,CB=CD,∠EBD=75°,则∠A的度数是( )
如图,点B、C在∠DAE的边上,AB=AC,CB=CD,∠EBD=75°,则∠A的度数是( )
 如图,点B、C在∠DAE的边上,AB=AC,CB=CD,∠EBD=75°,则∠A的度数是( )
如图,点B、C在∠DAE的边上,AB=AC,CB=CD,∠EBD=75°,则∠A的度数是( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
18.在直角坐标系中,点A(a,3)与点B(-4,b)关于y轴对称,则a+b的值是( )
| A. | -7 | B. | -1 | C. | 1 | D. | 7 |
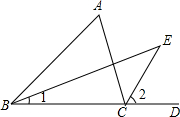 请在下列证明过程中,标注恰当的理由.如图,在△ABC中,∠ABC的平分线BE与∠ACD的平分线CE相交于点E.
请在下列证明过程中,标注恰当的理由.如图,在△ABC中,∠ABC的平分线BE与∠ACD的平分线CE相交于点E.
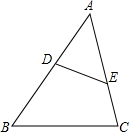 如图,点D、E分别在AB、AC上,且∠B=∠AED,若DE=4,AE=6,BC=8,则AB的长为12.
如图,点D、E分别在AB、AC上,且∠B=∠AED,若DE=4,AE=6,BC=8,则AB的长为12.