题目内容
10.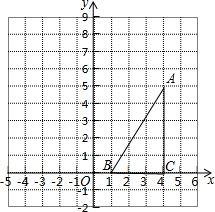 如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度后,再沿y轴向上平移2个单位,根据所给的直角坐标系(O是坐标原点),解答下列问题:
如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度后,再沿y轴向上平移2个单位,根据所给的直角坐标系(O是坐标原点),解答下列问题:(1)画出两次平移后的三角形A′B′C′;
(2)先写出A′,B′,C′三点的坐标,再求出三角形AA′C′的面积.
分析 (1)直接利用平移的性质得出对应点位置,进而得出答案;
(2)利用三角形面积求法直接得出答案.
解答  解:(1)如图所示:△A′B′C′即为所求;
解:(1)如图所示:△A′B′C′即为所求;
(2)A′(-1,7),B′(-4,2),C′(-1,2);
S△AA′C′=$\frac{1}{2}$×(7-2)×[4-(-1)]
=$\frac{1}{2}$×5×5
=$\frac{25}{2}$.
点评 此题主要考查了平移变换以及三角形面积求法,正确得出对应点位置是解题关键.

练习册系列答案
相关题目
1.下列说法正确的是( )
| A. | 经过两点可以画无数条直线 | |
| B. | 两条射线组成的图形叫做角 | |
| C. | 正多边形的各边都相等,各角都相等 | |
| D. | 两个锐角的和一定大于直角 |
18.线段CD是由线段AB平移得到的,点A(-1,4)的对应点为C(-1,7),则点B(-4,-1)的对应点D的坐标为( )
| A. | (2,9) | B. | (5,3) | C. | (-4,2) | D. | (-9,-4) |
 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=10,BC=16,则EF的长为3.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=10,BC=16,则EF的长为3.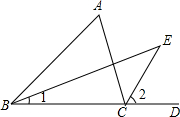 请在下列证明过程中,标注恰当的理由.如图,在△ABC中,∠ABC的平分线BE与∠ACD的平分线CE相交于点E.
请在下列证明过程中,标注恰当的理由.如图,在△ABC中,∠ABC的平分线BE与∠ACD的平分线CE相交于点E.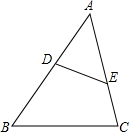 如图,点D、E分别在AB、AC上,且∠B=∠AED,若DE=4,AE=6,BC=8,则AB的长为12.
如图,点D、E分别在AB、AC上,且∠B=∠AED,若DE=4,AE=6,BC=8,则AB的长为12.