题目内容
1.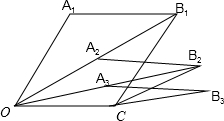 如图所示,平行四边形OA1B1C中,OA1=OC=1,∠A1OC=60°,记为第一个平行四边形,A2是对角线OB1的中点,以OA2和OC为边,再做平行四边形OA2B2C,依此类推,第三个平行四边形的面积为$\frac{\sqrt{3}}{8}$;第n个平行四边形的面积为$\frac{\sqrt{3}}{{2}^{n}}$.
如图所示,平行四边形OA1B1C中,OA1=OC=1,∠A1OC=60°,记为第一个平行四边形,A2是对角线OB1的中点,以OA2和OC为边,再做平行四边形OA2B2C,依此类推,第三个平行四边形的面积为$\frac{\sqrt{3}}{8}$;第n个平行四边形的面积为$\frac{\sqrt{3}}{{2}^{n}}$.
分析 连接A1C,过A1作A1D⊥OC于D,由OA1=OC=1,∠A1OC=60°,求得A1D=$\frac{\sqrt{3}}{2}$,于是得到S${\;}_{平行四边形O{A}_{1}{B}_{1}C}$=$\frac{\sqrt{3}}{2}$,由于A2是对角线OB1的中点,求出A2到OC的距离=$\frac{1}{2}$A1D=$\frac{\sqrt{3}}{4}$,于是得到第二个平行四边形的面积=$\frac{1}{2}$S${\;}_{平行四边形O{A}_{1}{B}_{1}C}$=$\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{{2}^{2}}$,即可找到规律得到结果.
解答 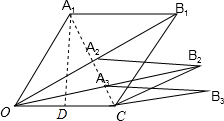 解:连接A1C,过A1作A1D⊥OC于D,
解:连接A1C,过A1作A1D⊥OC于D,
∵OA1=OC=1,∠A1OC=60°,
∴A1D=$\frac{\sqrt{3}}{2}$,
∴S${\;}_{平行四边形O{A}_{1}{B}_{1}C}$=$\frac{\sqrt{3}}{2}$,
∵A2是对角线OB1的中点,
∴A2到OC的距离=$\frac{1}{2}$A1D=$\frac{\sqrt{3}}{4}$,
∴第二个平行四边形的面积=$\frac{1}{2}$S${\;}_{平行四边形O{A}_{1}{B}_{1}C}$=$\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{{2}^{2}}$,
∴第三个平行四边形的面积=$\frac{1}{2}$第二个平行四边形的面积=$\frac{\sqrt{3}}{8}$=$\frac{\sqrt{3}}{{2}^{3}}$,
∴第n个平行四边形的面积=$\frac{\sqrt{3}}{{2}^{n}}$.
故答案为:$\frac{\sqrt{3}}{8}$,$\frac{\sqrt{3}}{{2}^{n}}$.
点评 本题考查了平行四边形的性质,平行四边形的面积,熟练掌握平行四边形的性质定理是解题的关键.

 如图所示,此图的俯视图为( )
如图所示,此图的俯视图为( )| A. |  | B. |  | C. |  | D. |  |
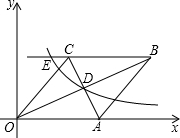 如图:已知,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0),经过D点,交BC的延长线于E点,E点的坐标是(5,8).
如图:已知,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0),经过D点,交BC的延长线于E点,E点的坐标是(5,8).
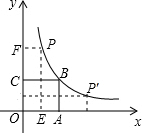 如图,正方形OABC的面积为16,点O为坐标原点,点B在双曲线y=$\frac{k}{x}$(x>0)上,点P(m,n)是双曲线上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF在正方形OABC之外部分的面积为S.
如图,正方形OABC的面积为16,点O为坐标原点,点B在双曲线y=$\frac{k}{x}$(x>0)上,点P(m,n)是双曲线上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF在正方形OABC之外部分的面积为S.