题目内容
11.先化简,再求值:$\frac{12-3x}{x-2}$÷(x+2-$\frac{12}{x-2}$)•$\frac{{x}^{2}+8x+16}{3}$,其中x=3tan30°-8cos60°.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值,把x的值代入进行计算即可.
解答 解:原式=$\frac{3(4-x)}{x-2}$÷$\frac{{x}^{2}-4-12}{x-2}$•$\frac{(x+4)^{2}}{3}$
═$\frac{3(4-x)}{x-2}$•$\frac{x-2}{(x+4)(x-4)}$•$\frac{(x+4)^{2}}{3}$
=-x-4
∵x=3tan30°-8cos60°=3×$\frac{\sqrt{3}}{3}$-8×$\frac{1}{2}$=$\sqrt{3}$-4,
∴原式=4-$\sqrt{3}$-4
=-$\sqrt{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.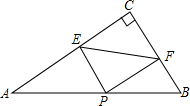 如图,在△ABC中,AB=10,BC=6,AC=8,PE⊥AC于E,PF⊥BC于F.则线段EF长的最小值为( )
如图,在△ABC中,AB=10,BC=6,AC=8,PE⊥AC于E,PF⊥BC于F.则线段EF长的最小值为( )
 如图,在△ABC中,AB=10,BC=6,AC=8,PE⊥AC于E,PF⊥BC于F.则线段EF长的最小值为( )
如图,在△ABC中,AB=10,BC=6,AC=8,PE⊥AC于E,PF⊥BC于F.则线段EF长的最小值为( )| A. | 5 | B. | $\frac{3}{2}$ | C. | 4 | D. | $\frac{24}{5}$ |
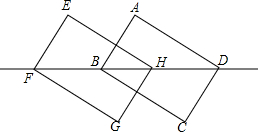 如图,在长方形ABCD中,AB=CD=6,AD=BC=8,对角线BD=10,现将长方形沿对角线BD所在直线向左平移4个单位得到长方形EFGH,则点F到直线AD的距离是( )
如图,在长方形ABCD中,AB=CD=6,AD=BC=8,对角线BD=10,现将长方形沿对角线BD所在直线向左平移4个单位得到长方形EFGH,则点F到直线AD的距离是( )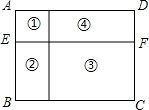 如图,要用60m的篱笆在一块足够大的空地上围出四个花园,已知①号花园为正方形,且④号花园的周长等于①号和②号花园周长之和.设CD的长为xm,②号花园的面积为ym2.
如图,要用60m的篱笆在一块足够大的空地上围出四个花园,已知①号花园为正方形,且④号花园的周长等于①号和②号花园周长之和.设CD的长为xm,②号花园的面积为ym2.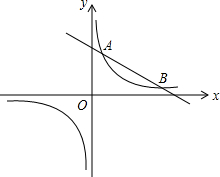 如图,双曲线y=$\frac{k}{x}$(k>0)与直线y=-$\frac{1}{2}$x+4相交于A,B两点.
如图,双曲线y=$\frac{k}{x}$(k>0)与直线y=-$\frac{1}{2}$x+4相交于A,B两点.