题目内容
10.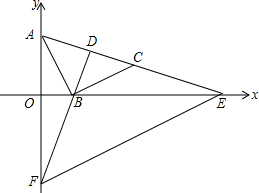 如图,在平面直角坐标系中,点A的坐标为(0,2),点B在x轴的正半轴上,以AB为直角边在第一象限内作等腰直角△ABC,延长AC交x轴的正半轴于E点,D为AC的中点,连接DB并延长交y轴负半轴于F,F的坐标为(0,m),连接EF.
如图,在平面直角坐标系中,点A的坐标为(0,2),点B在x轴的正半轴上,以AB为直角边在第一象限内作等腰直角△ABC,延长AC交x轴的正半轴于E点,D为AC的中点,连接DB并延长交y轴负半轴于F,F的坐标为(0,m),连接EF.(1)若点B的坐标为(1,0)
①求点C的坐标;
②求△AEF的面积(用含有m的式子表示).
(2)是否存在m,使得△BCE为等腰三角形?若存在,请求出m;若不存在,请说明理由.
分析 (1)①作CH⊥BE于H,根据全等三角形的判定定理证明△ABO≌△BCH,得到CH=OB=1,BH=OA=2,求出点C的坐标;
②证明△ADF∽△BDE,根据AD=BD得到AF=BE,根据三角形的面积公式计算即可;
(2)根据题意确定△BCE为等腰三角形时,只有CB=CE,根据等腰三角形的性质得到关于m的方程,解方程即可得到答案.
解答 解:(1)①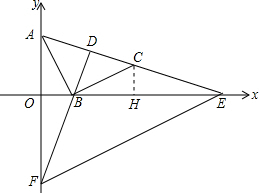 作CH⊥BE于H,
作CH⊥BE于H,
∵∠ABO+∠OAB=90°,∠ABO+∠HBC=90°,
∴∠OAB=∠HBC,
在△ABO和△BCH中,
$\left\{\begin{array}{l}{∠OAB=∠HBC}\\{∠AOB=∠BHC}\\{AB=BC}\end{array}\right.$,
∴△ABO≌△BCH,
∴CH=OB=1,BH=OA=2,
则OH=3,
∴点C的坐标为(3,1);
②∵△ABC是等腰直角三角形,D为AC的中点,
∴BD⊥AC,
∴∠AFD+∠FAD=90°,又∠FAD+∠AEO=90°,
∴∠AFD=∠AEO,又∠ADF=∠AOE=90°,
∴△ADF∽△BDE,
∴$\frac{AD}{BD}$=$\frac{AF}{BE}$,又AD=BD,
∴AF=BE,
∵AF=2-m,
∴BE=2-m,OE=3-m,
∴△AEF的面积=$\frac{1}{2}$×AF×OE=$\frac{1}{2}$(2-m)(3-m)=$\frac{1}{2}$m2-$\frac{5}{2}$m+3;
(2)∵∠BCE=180°-45°=135°,
∴△BCE为等腰三角形时,只有CB=CE,
∴BH=HE,又BH=OA=2,
∴BE=4,
由②得,BE=AF,
∴2-m=4,
解得,m=-2,
答:当m=-2时,△BCE为等腰三角形.
点评 本题考查的是等腰直角三角形的性质和等腰三角形的判定以及相似三角形的判定和性质,正确理解坐标与图形的关系、灵活运用相关的定理是解题的关键.

| A. | 12cm | B. | 10cm | C. | 8cm | D. | 6cm |
 如图所示,AB比AC长2cm,BC的垂直平分线交AB于D,交BC于E,△ACD的周长是14cm,AB的长为8cm.
如图所示,AB比AC长2cm,BC的垂直平分线交AB于D,交BC于E,△ACD的周长是14cm,AB的长为8cm. 如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,∠A=90°,求四边形ABCD的面积.
如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,∠A=90°,求四边形ABCD的面积.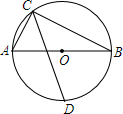 如图,⊙O的直径AB为13cm,弦AC为5cm,∠ACB的平分线交⊙O于D,则CD长是$\frac{17\sqrt{2}}{2}$cm.
如图,⊙O的直径AB为13cm,弦AC为5cm,∠ACB的平分线交⊙O于D,则CD长是$\frac{17\sqrt{2}}{2}$cm.