题目内容
19.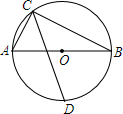 如图,⊙O的直径AB为13cm,弦AC为5cm,∠ACB的平分线交⊙O于D,则CD长是$\frac{17\sqrt{2}}{2}$cm.
如图,⊙O的直径AB为13cm,弦AC为5cm,∠ACB的平分线交⊙O于D,则CD长是$\frac{17\sqrt{2}}{2}$cm.
分析 首先作DF⊥CA,交CA的延长线于点F,作DG⊥CB于点G,连接DA,DB.由CD平分∠ACB,根据角平分线的性质得出DF=DG,由HL证明△AFD≌△BGD,得出CF的长,又△CDF是等腰直角三角形,从而求出CD的长.
解答 解:作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB.
∵CD平分∠ACB,
∴∠ACD=∠BCD
∴DF=DG,$\widehat{AD}=\widehat{BD}$,
∴DA=DB.
∵∠AFD=∠BGD=90°,
在Rt△ADF和Rt△BDG,
$\left\{\begin{array}{l}{AD=BD}\\{DF=DG}\end{array}\right.$,
∴Rt△AFD≌Rt△BGD(HL),
∴AF=BG.
同理:Rt△CDF≌Rt△CDG(HL),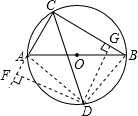
∴CF=CG.
∵AB是直径,
∴∠ACB=90°,
∵AC=5cm,AB=13cm,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=12(cm),
∴5+AF=12-AF,
∴AF=$\frac{7}{2}$,
∴CF=$\frac{17}{2}$,
∵CD平分∠ACB,
∴∠ACD=45°,
∵△CDF是等腰直角三角形,
∴CD=$\frac{17\sqrt{2}}{2}$(cm).
故答案为:$\frac{17\sqrt{2}}{2}$.
点评 本题综合考查了圆周角的性质,圆心角、弧、弦的对等关系,全等三角形的判定,角平分线的性质等知识点的运用.注意准确作出辅助线是解此题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
14.如图,图案均是用长度相等的小木棒,按一定规律拼撘而成,第一个图案需4根小木棒,则第6个图案小木棒根数是( )


| A. | 42 | B. | 48 | C. | 54 | D. | 56 |
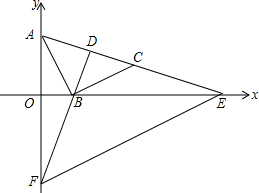 如图,在平面直角坐标系中,点A的坐标为(0,2),点B在x轴的正半轴上,以AB为直角边在第一象限内作等腰直角△ABC,延长AC交x轴的正半轴于E点,D为AC的中点,连接DB并延长交y轴负半轴于F,F的坐标为(0,m),连接EF.
如图,在平面直角坐标系中,点A的坐标为(0,2),点B在x轴的正半轴上,以AB为直角边在第一象限内作等腰直角△ABC,延长AC交x轴的正半轴于E点,D为AC的中点,连接DB并延长交y轴负半轴于F,F的坐标为(0,m),连接EF.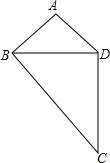 如图,已知AB=4,BC=9,BD=6,$\frac{AD}{DC}$=$\frac{2}{3}$,求证:BD平分∠ABC.
如图,已知AB=4,BC=9,BD=6,$\frac{AD}{DC}$=$\frac{2}{3}$,求证:BD平分∠ABC.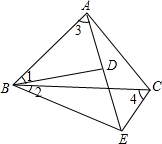 如图,∠1=∠2,∠3=∠4,试问:BD•AC=AB•DE成立吗?说说你的理由.
如图,∠1=∠2,∠3=∠4,试问:BD•AC=AB•DE成立吗?说说你的理由.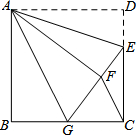 如图,在正方形ABCD中,AB=12,点E在边CD上,CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.有下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=6.其中正确的结论是①②③.
如图,在正方形ABCD中,AB=12,点E在边CD上,CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.有下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=6.其中正确的结论是①②③.