题目内容
1.数轴上表示1,$\sqrt{2}$的点为A,B,且C、B两点到点A的距离相等,则点C所表示的数2-$\sqrt{2}$.分析 设C点表示的数是c,再由数轴上两点间的距离公式即可得出结论.
解答 解:设C点表示的数是c,则|c-1|=|$\sqrt{2}$-|,解得c=$\sqrt{2}$(舍去)或c=2-$\sqrt{2}$.
故答案为:2-$\sqrt{2}$.
点评 本题考查的是实数与数轴,熟知数轴上各点与实数是一一对应关系是解答此题的关键.

练习册系列答案
相关题目
16.下列各组数中,数值相等的是( )
| A. | 32和23 | B. | -23和(-2)3 | C. | -|23|和|-23| | D. | -32和(-3)2 |
6.解分式方程$\frac{1}{2x-3}$-4=$\frac{5}{3-2x}$时,去分母后可得( )
| A. | 1-4(2x-3)=-5 | B. | 1-4(2x-3)=5 | C. | 2x-3-4=-5 | D. | 2x-3-4=5(2x-3) |
13.$\sqrt{(-25)^{2}}$的平方根为( )
| A. | 5 | B. | -5 | C. | ±5 | D. | 25 |
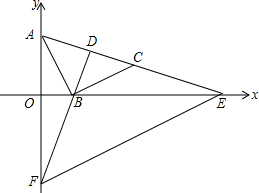 如图,在平面直角坐标系中,点A的坐标为(0,2),点B在x轴的正半轴上,以AB为直角边在第一象限内作等腰直角△ABC,延长AC交x轴的正半轴于E点,D为AC的中点,连接DB并延长交y轴负半轴于F,F的坐标为(0,m),连接EF.
如图,在平面直角坐标系中,点A的坐标为(0,2),点B在x轴的正半轴上,以AB为直角边在第一象限内作等腰直角△ABC,延长AC交x轴的正半轴于E点,D为AC的中点,连接DB并延长交y轴负半轴于F,F的坐标为(0,m),连接EF.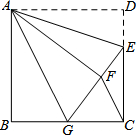 如图,在正方形ABCD中,AB=12,点E在边CD上,CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.有下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=6.其中正确的结论是①②③.
如图,在正方形ABCD中,AB=12,点E在边CD上,CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.有下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=6.其中正确的结论是①②③.